`@` `\text {Ans}`

`\downarrow`

Gửi c!

Bài 1: 

a) \(3x^2\left(2x^3-x+5\right)-6x^5-3x^3+10x^2\)

\(=6x^5-3x^3+10x^2-6x^5-3x^3+10x^2\)

\(=10x^2+10x^2\)

\(=20x^2\)

b) \(-2x\left(x^3-3x^2-x+11\right)-2x^4+3x^3+2x^2-22x\)

\(=-2x^4+6x^3+2x^2-22x-2x^4+3x^3+2x^2-22x\)

\(=-4x^4+9x^3+4x^2-44x\)

`a)``P(x)=2x^3-2x+x^2+3x+2`

`=2x^3+x^2+x+2`

`Q(x)=4x^3-3x^2-3x+4x-3x^3+4x^2+1`

`=x^3+x^2+x+1`

`#Khói`

a)\(P\left(x\right)=2x^3-2x+x^2+3x+2\)

\(P\left(x\right)=2x^3+x^2+x+2\)

\(Q\left(x\right)=4x^3-3x^2-3x+4x-3x^3+4x^2+1\)

\(Q\left(x\right)=x^3+x^2+x+1\)

a) 2x(x+3) – 3x²(x+2) + x(3x² + 4x – 6)

= (2x . x + 2x . 3) – (3x² . x + 3x² . 2) + (x . 3x² + x . 4x – x . 6)

= 2x² + 6x – (3x³ + 6x²) + (3x³ + 4x² - 6x)

= 2x² + 6x – 3x³ – 6x² + 3x³ + 4x² - 6x

= (– 3x³ + 3x³ ) + (2x²  - 6x² + 4x² ) + (6x – 6x)

= 0 + 0 + 0

= 0

b) 3x(2x² – x) – 2x²(3x+1) + 5(x² – 1)

= [3x . 2x² + 3x . (-x)] – (2x² . 3x + 2x² . 1) + [5x² + 5 . (-1)]

= 6x³ – 3x² – (6x³ +2x²) + 5x² – 5

= 6x³ – 3x² – 6x³ - 2x² + 5x² – 5

= (6x³ – 6x³ ) + (-3x² – 2x² + 5x²) – 5

= 0 + 0 – 5

= - 5

Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:

* Ta có: f(x) = x7 – 3x2 – x5 + x4 – x2 + 2x – 7

            = x7 - (3x2+ x2) – x5+ x4 + 2x – 7

            = x7 – 4x2 – x5+ x4 + 2x – 7

            = x7 – x5 + x4 – 4x2 + 2x - 7

g(x) = x – 2x2 + x4 – x5 – x7 – 4x2 – 1

            = x – ( 2x2 + 4x2) + x4 – x5 –x7 – 1

            = x – 6x2 + x4 – x5 – x7 – 1

            = -x7 – x5 + x4 – 6x2 + x – 1

* f(x) – g(x)

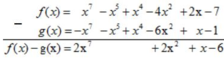
Vậy f(x) – g(x) = 2x7 + 2x2 + x - 6

\(\begin{array}{l}a){\rm{ }}3{x^2}-{\rm{ }}3x\left( {x{\rm{ }}-{\rm{ }}2} \right){\rm{ }} = {\rm{ }}36\\ \Leftrightarrow 3{x^2}-{\rm{ [}}3x.x + 3x.( - 2)] = 36\\ \Leftrightarrow 3{x^2} - (3{x^2} - 6x) = 36\\ \Leftrightarrow 3{x^2} - 3{x^2} + 6x = 36\\ \Leftrightarrow 6x = 36\\ \Leftrightarrow x = 36:6\\ \Leftrightarrow x = 6\end{array}\)

Vậy x = 6

\(\begin{array}{l}b){\rm{ }}5x\left( {4{x^2}-{\rm{ }}2x{\rm{ }} + {\rm{ }}1} \right){\rm{ }}-{\rm{ }}2x\left( {10{x^2}-{\rm{ }}5x{\rm{ }} + {\rm{ }}2} \right){\rm{ }} = {\rm{ }} - 36\\ \Leftrightarrow 5x.4{x^2} + 5x.( - 2x) + 5x.1 - [2x.10{x^2} + 2x.( - 5x) + 2x.2] =  - 36\\ \Leftrightarrow 20{x^3} - 10{x^2} + 5x - (20{x^3} - 10{x^2} + 4x) =  - 36\\ \Leftrightarrow 20{x^3} - 10{x^2} + 5x - 20{x^3} + 10{x^2} - 4x =  - 36\\ \Leftrightarrow (20{x^3} - 20{x^3}) + ( - 10{x^2} + 10{x^2}) + (5x - 4x) =  - 36\\ \Leftrightarrow x =  - 36\end{array}\)

Vậy x = -36

Lời giải:

1.

$4x+9=0$

$4x=-9$

$x=\frac{-9}{4}$
2.

$-5x+6=0$

$-5x=-6$

$x=\frac{6}{5}$

3.

$x^2-1=0$

$x^2=1=1^2=(-1)^2$

$x=\pm 1$

4.

$x^2-9=0$

$x^2=9=3^2=(-3)^2$

$x=\pm 3$

5.

$x^2-x=0$

$x(x-1)=0$

$x=0$ hoặc $x-1=0$

$x=0$ hoặc $x=1$

6.

$x^2-2x=0$

$x(x-2)=0$

$x=0$ hoặc $x-2=0$

$x=0$ hoặc $x=2$

7.

$x^2-3x=0$

$x(x-3)=0$

$x=0$ hoặc $x-3=0$ 

$x=0$ hoặc $x=3$

8.

$3x^2-4x=0$

$x(3x-4)=0$

$x=0$ hoặc $3x-4=0$

$x=0$ hoặc $x=\frac{4}{3}$

a) \(...=P\left(x\right)=2x^4-x^4+3x^3+4x^2-3x^2+3x-x+3\)

\(P\left(x\right)=x^4+3x^3+x^2+2x+3\)

\(...=Q\left(x\right)=x^4+x^3+3x^2-x^2+4x+4-2\)

\(Q\left(x\right)=x^4+x^3+2x^2+4x+2\)

b) \(P\left(x\right)+Q\left(x\right)=\left(x^4+3x^3+x^2+2x+3\right)+\left(x^4+x^3+2x^2+4x+2\right)\)

\(\Rightarrow P\left(x\right)+Q\left(x\right)=2x^4+4x^3+3x^2+6x+5\)

\(P\left(x\right)-Q\left(x\right)=\left(x^4+3x^3+x^2+2x+3\right)-\left(x^4+x^3+2x^2+4x+2\right)\)

\(\)\(\Rightarrow P\left(x\right)-Q\left(x\right)=x^4+3x^3+x^2+2x+3-x^4-x^3-2x^2-4x-2\)

\(\Rightarrow P\left(x\right)-Q\left(x\right)=2x^3-x^2-2x+1\)

a) Đặt A(x)=0

\(\Leftrightarrow-4x-5=0\)

\(\Leftrightarrow-4x=5\)

hay \(x=-\dfrac{5}{4}\)

b) Đặt B(x)=0

\(\Leftrightarrow3\left(2x-1\right)-2\left(x+1\right)=0\)

\(\Leftrightarrow6x-3-2x-2=0\)

\(\Leftrightarrow4x=5\)

hay \(x=\dfrac{5}{4}\)