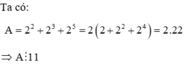Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(A=11...122...2=11...100...0+22...2\) ( 100 c/s 1 ; 100 c/s 0 ; 100 c/s 2 )
\(=11...1.\left(100...0+2\right)\) ( 100 c/s 1 ; 100 c/s 0 )
\(=11...1.\left(3.33...34\right)\) ( 100 c/s 1 ; 99 c/s 3 )
\(=33...3.33...34\) ( 100 c/s 3 ; 99 c/s 3 )
Vậy A là tích của hai STN liên tiếp

1)Ta có:
\(111...11222...22\left(100 cs 1 v\text{à} 2\right)=10^{100}.111...111\left(100 cs 1\right)+222...22\left(100 cs 2\right)\)
\(=10^{100}.\frac{10^{100}-1}{9}+2.\frac{10^{100}-1}{9}=\frac{10^{100}\left(10^{100}-1\right)+2\left(10^{100}-1\right)}{9}=\frac{\left(10^{100}+2\right)\left(10^{100}-1\right)}{9}=\frac{10^{100}+2}{3}.\frac{10^{100}-1}{3}\)
\(M\text{à} \frac{10^{100}+2}{3}\ne\frac{10^{100}-1}{3} \)
\(\Rightarrow111...11222..2\left(100 cs 1 v\text{à} 2\right) \) không phải là tích 2 số tự nhiên
2) Để dacb chia hết cho 4 thì cb chia hết cho 4
Ta có :
cb=10c+b=8c+2c+b
Mà 8c chia hết cho 4 nên
2c+b cũng phải chia hết cho 4(đpcm)

Lời giải:
Đặt \(\underbrace{111....1}_{100}=a\Rightarrow 9a+1=1\underbrace{000...0}_{100}\)
Khi đó:
\(\underbrace{1111....1}_{100}\underbrace{222....2}=\underbrace{111...1}_{100}\times 1\underbrace{00...0}_{100}+\underbrace{222....2}_{100}\)
\(a(9a+1)+2a=9a^2+3a=3a(3a+1)\) là tích của 2 số
tự nhiên liên tiếp $3a, 3a+1$
Ta có đpcm.

Sơ đồ con đường |
Lời giải chi tiết |
Bước 1. Phân tích sao cho tổng đó thành tích các thừa số trong đó có một thừa số chia hết cho 11. Bước 2. Áp dụng tính chất chia hết của một tích. |
Ta có: A = 2 2 + 2 3 + 2 6 = 2 2 + 2 2 + 2 4 = 2.22 ⇒ A ⋮ 11 |

1) Ta có : 11a + 22b + 33c
= 11a + 11.2b + 11.3c
= 11.(a + 2b + 3c) \(⋮\)11
=> 11a + 22b + 33c \(⋮\)11
2) 2 + 22 + 23 + ... + 2100
= (2 + 22) + (23 + 24) + ... + (299 + 2100)
= (2 + 22) + 22.(2 + 22) + ... + 298.(2 + 22)
= 6 + 22.6 + ... + 298.6
= 6.(1 + 22 + .. + 298)
= 2.3.(1 + 22 + ... + 298) \(⋮\)3
=> 2 + 22 + 23 + ... + 2100 \(⋮\)3
3) Ta có: abcabc = abc000 + abc
= abc x 1000 + abc
= abc x (1000 + 1)
= abc x 1001
= abc .7. 13.11 (1)
= abc . 7 . 13 . 11 \(⋮\)7
=> abcabc \(⋮\)7
=> Từ (1) ta có : abcabc = abc x 7.11.13 \(⋮\)11
=> abcabc \(⋮\)11
=> Từ (1) ta có : abcabc = abc . 7.11.13 \(⋮\) 13
=> => abcabc \(⋮\)13
1
.\(11a+22b+33c=11\left(a+2b+3c\right)⋮11\)
\(\Rightarrow11a+22b+33c⋮11\left(đpcm\right)\)
hc tốt