
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{9+3+4+5}\)
=\(\sqrt{21}\)
=4,582575695
ai k mình mình k lại

g: \(\text{Δ}=\left(-6\right)^2-4\left(2m+1\right)=36-8m-4=-8m+32\)
Để phương trình có hai nghiệm thì -8m+32>=0
=>m<=4
Để phương trình có hai nghiệm cùng âm thì:
\(\left\{{}\begin{matrix}m< =4\\\dfrac{-\left(-6\right)}{1}< 0\\2m+1>0\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
h: \(\left\{{}\begin{matrix}2x_1-x_2=15\\x_1+x_2=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=7\\x_2=-1\end{matrix}\right.\)
x1*x2=2m+1
=>2m+1=-7
=>2m=-8
=>m=-4
i: \(x_1^2+x_2^2=5\)
=>(x1+x2)^2-2x1x2=5
=>6^2-2(2m+1)=5
=>36-4m-2=5
=>34-4m=5
=>4m=29
=>m=29/4(loại)
j: \(x_1^3+x_2^3=5\)
=>\(\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=5\)
=>\(6^3-3\cdot6\cdot\left(2m+1\right)=5\)
=>216-18(2m+1)=5
=>18(2m+1)=211
=>2m+1=211/18
=>2m=193/18
=>m=193/36(loại)

A=P^2-P
\(=\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}-2\right)^2}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\)
\(=\dfrac{x+2\sqrt{x}+1-x+\sqrt{x}+2}{\left(\sqrt{x}-2\right)^2}=\dfrac{3\sqrt{x}+3}{\left(\sqrt{x}-2\right)^2}>=0\)
=>P^2>=P

a: 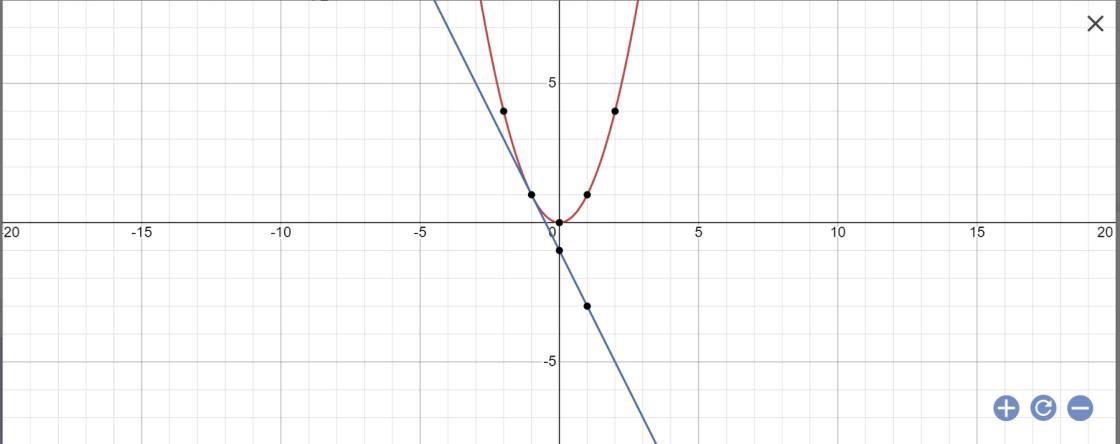
b: PTHĐGĐ là:
x^2=-2x-1
=>x^2+2x+1=0
=>(x+1)^2=0
=>x=-1
Khi x=-1 thì y=(-1)^2=1

1: \(A=\dfrac{\left(x+1\right)^3}{\left(x+1\right)^2}=x+1\)
\(B=\dfrac{\left(x+1\right)\cdot\left(x^2-x+1\right)}{x+1}=x^2-x+1\)
2: A=B
=>x^2-x+1=x+1
=>x^2-2x=0
=>x=0 hoặc x=2

Hình vẽ nhỏ quá. Bạn nên gõ đề bằng công thức toán để được hỗ trợ tốt hơn.


 giup minh cau nay voi a
giup minh cau nay voi a


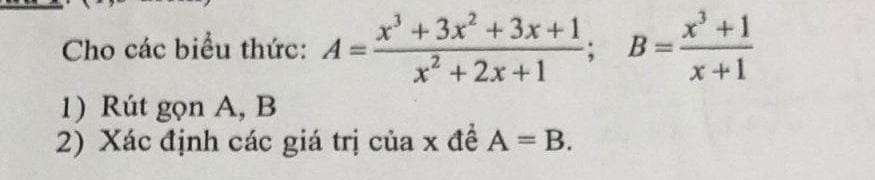
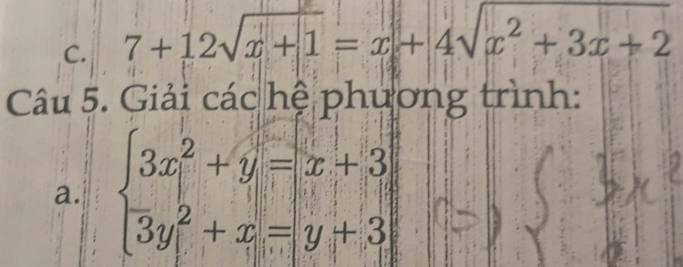
Bạn cần bài nào thì bạn nên ghi chú rõ ra nhé.