
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
Xét ΔABC vuông tại C có
\(CB=BA\cdot\sin60^0=12\cdot\dfrac{\sqrt{3}}{2}=6\sqrt{3}\left(cm\right)\)

Bài 3 :
\(\Leftrightarrow\sqrt{9x^2-6x+1}=\sqrt{\left(3x-1\right)^2}=\left|3x-1\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=5\\3x-1=-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy ...
Bài 5 :
Ta có :\(x-5\sqrt{x}+7=x-2.\sqrt{x}.\dfrac{5}{2}+\dfrac{25}{4}+\dfrac{3}{4}=\left(\sqrt{x}-\dfrac{5}{2}\right)^2+\dfrac{3}{4}\)
Thấy : \(\left(\sqrt{x}-\dfrac{5}{2}\right)^2\ge0\)
\(\Rightarrow\left(\sqrt{x}-\dfrac{5}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
\(\Rightarrow P=\dfrac{1}{x-5\sqrt{x}+7}=\dfrac{1}{\left(\sqrt{x}-\dfrac{5}{2}\right)^2+\dfrac{3}{4}}\le\dfrac{1}{\dfrac{3}{4}}=\dfrac{4}{3}\)
Vậy \(Max_P=\dfrac{4}{3}\Leftrightarrow\sqrt{x}-\dfrac{5}{2}=0\Leftrightarrow x=\dfrac{25}{4}\)
Bài 1:
a) Ta có: \(\sqrt{25}\cdot\sqrt{144}+\sqrt[3]{-27}-\sqrt[3]{216}\)
\(=5\cdot12-3-6\)
\(=60-9=51\)
b) Ta có: \(\sqrt{8.1\cdot360}\)
\(=\sqrt{8.1\cdot10\cdot36}\)
\(=\sqrt{81\cdot36}\)
\(=9\cdot6=54\)
Bài 2:
a) Ta có: \(\sqrt{80}-\sqrt{\left(2-\sqrt{5}\right)^2}+\sqrt{3\dfrac{1}{5}}\)
\(=4\sqrt{5}-\sqrt{5}+2+\dfrac{4}{\sqrt{5}}\)
\(=3\sqrt{5}+2+\dfrac{4\sqrt{5}}{5}\)
\(=\dfrac{10+19\sqrt{5}}{5}\)
b) Ta có: \(\dfrac{\sqrt{6}-\sqrt{3}}{1-\sqrt{2}}+\dfrac{3+6\sqrt{3}}{\sqrt{3}}-\dfrac{13}{\sqrt{3}+4}\)
\(=\dfrac{-\sqrt{3}\left(1-\sqrt{2}\right)}{1-\sqrt{2}}+\dfrac{\sqrt{3}\left(\sqrt{3}+6\right)}{\sqrt{3}}-\dfrac{13\left(4-\sqrt{3}\right)}{\left(4+\sqrt{3}\right)\left(4-\sqrt{3}\right)}\)
\(=-\sqrt{3}+\sqrt{3}+6-4+\sqrt{3}\)
\(=2+\sqrt{3}\)



Bài 2:
\(\sqrt{2x-1}=5\)
=> 2x - 1 = 25
=> 2x = 26
=> x = 13
b) \(\sqrt[3]{3x+2}=-3\)
=> 3x + 2 = -27
=> 3x = -29
=> x = -29/3
P/s: Mỗi lần chỉ đc hỏi 1 bài thôi em nehs!
1. ĐK:
a, \(x\ge\dfrac{5}{2}\)
b, \(\left\{{}\begin{matrix}x\ge0\\x\ne\dfrac{9}{4}\end{matrix}\right.\)
2.
a,ĐK: \(x\ge\dfrac{1}{2}\)
PT\(\Leftrightarrow2x-1=25\Rightarrow x=13\left(tm\right)\)
b,ĐK: \(\forall x\in R\)
PT\(\Leftrightarrow3x+2=-27=>x=-\dfrac{29}{3}\) (tm)
3.
a,\(\sqrt{5}.\sqrt{1,2}.\sqrt{24}=\sqrt{120}.\sqrt{1,2}=12\)
b,\(\dfrac{\sqrt{4444}}{\sqrt{1111}}=\dfrac{\sqrt{4}.\sqrt{1111}}{\sqrt{1111}}=2\)
c,\(\sqrt{\dfrac{3}{5}}+\sqrt{\dfrac{5}{3}}-\dfrac{1}{2}\sqrt{60}=\dfrac{8}{\sqrt{15}}-\sqrt{15}=-\dfrac{7}{\sqrt{15}}\)
d,\(\sqrt{5+2\sqrt{6}}+\sqrt{5-2\sqrt{6}}=\sqrt{3}+\sqrt{2}+\sqrt{3}-\sqrt{2}=2\sqrt{3}\)

Bài 1:
c: Vì a+b+c=0 nên phương trình có hai nghiệm phân biệt là
x1=1; \(x2=\dfrac{c}{a}=\dfrac{3\sqrt{2}+1}{1-\sqrt{2}}\)

a: \(\left\{{}\begin{matrix}3x+6y=4\\x+4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{3}\\x=\dfrac{2}{3}\end{matrix}\right.\)

a: \(\left\{{}\begin{matrix}3x+6y=4\\x+4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+6y=4\\3x+12y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-6y=-2\\x+4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{3}\\x=\dfrac{2}{3}\end{matrix}\right.\)

Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)

a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại B có BH là đường cao ứng với cạnh huyền AC, ta được:
\(BH^2=HA\cdot HC\)
\(\Leftrightarrow BH^2=2\cdot6=12\)
hay \(BH=2\sqrt{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔBHA vuông tại H, ta được:
\(BA^2=BH^2+HA^2\)
\(\Leftrightarrow AB^2=\left(2\sqrt{3}\right)^2+2^2=12+4=16\)
hay BA=4(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại B, ta được:
\(AC^2=BA^2+BC^2\)
\(\Leftrightarrow BC^2=8^2-4^2=48\)
hay \(BC=4\sqrt{3}\left(cm\right)\)
b) Xét ΔABC vuông tại B có
\(\sin\widehat{A}=\dfrac{BC}{CA}=\dfrac{4\sqrt{3}}{8}=\dfrac{\sqrt{3}}{2}\)
\(\cos\widehat{A}=\dfrac{BA}{CA}=\dfrac{4}{8}=\dfrac{1}{2}\)




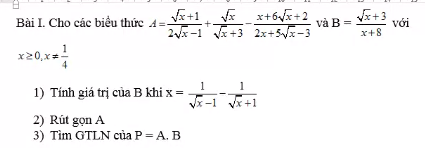




 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Câu 1 :
a) Ta có : \(P\text{=}\left(\dfrac{a\sqrt{a}-1}{a-\sqrt{a}}-\dfrac{a\sqrt{a}+1}{a+\sqrt{a}}\right):\dfrac{a+2}{a-2}\)
\(P\text{=}\left(\dfrac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a\left(\sqrt{a}+1\right)}}\right):\dfrac{a+2}{a-2}\)
\(P\text{=}\left(\dfrac{a+\sqrt{a}+1}{\sqrt{a}}-\dfrac{a-\sqrt{a}+1}{\sqrt{a}}\right):\dfrac{a+2}{a-2}\)
\(P\text{=}\dfrac{2\sqrt{a}}{\sqrt{a}}:\dfrac{a+2}{a-2}\)
\(P\text{=}2:\dfrac{a+2}{a-2}\text{=}\dfrac{2.\left(a-2\right)}{a+2}\)
b) Để P có giá trị nguyên \(\Leftrightarrow\dfrac{2.\left(a-2\right)}{a+2}\in Z\)
\(\Leftrightarrow\dfrac{2.\left(a+2\right)-8}{a+2}\in Z\)
\(\Leftrightarrow2-\dfrac{8}{a+2}\in Z\)
\(\Leftrightarrow\dfrac{8}{a+2}\in Z\Leftrightarrow\left(a+2\right)\inƯ\left(8\right)\)
Do đó ta có bảng
Vậy..........