Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(S=a^2+\dfrac{1}{a^2}=\left(\dfrac{1}{16}a^2+\dfrac{1}{a^2}\right)+\dfrac{15}{16}a^2\ge2.\sqrt{\dfrac{1}{16}a^2.\dfrac{1}{a^2}}+\dfrac{15}{16}.2^2=\dfrac{17}{4}\)
Dấu "=" xảy ra khi \(a=2\)
Vậy \(MinS=\dfrac{17}{4}\)

Ghi đề sai rồi nha bạn!
Đề: Cho \(a\ge2.\) Tìm giá trị nhỏ nhất của \(S=a+\frac{1}{a^2}\)
Lời giải:
Lựa chọn điểm rơi và áp dụng bđt \(AM-GM\) cho bộ \(3\) số không âm kết hợp với giả thiết \(a\ge2\), ta có:
\(S=a+\frac{1}{a^2}=\left(\frac{a}{8}+\frac{a}{8}+\frac{1}{a^2}\right)+\frac{6a}{8}\ge3\sqrt[3]{\frac{a}{8}.\frac{a}{8}.\frac{1}{a^2}}+\frac{6a}{8}=\frac{3}{4}+\frac{6a}{8}\ge\frac{3}{4}+\frac{6.2}{8}=\frac{9}{4}\)
Vậy, \(S_{min}=\frac{9}{4}\)
Dấu \("="\) xảy ra \(\Leftrightarrow\) \(a=2\)

`a)D` xác định `<=>a-1 ne 0<=>a ne 1`
`b)` Với `a ne 1` có:
`D=([a-1]/[a^2+a+1]-[1-3a+a^2]/[(a-1)(a^2+a+1)]-1/[a-1]).[1-a]/[a^2+1]`
`D=[(a-1)^2-1+3a-a^2-a^2-a-1]/[(a-1)(a^2+a+1)].[-(a-1)]/[a^2+1]`
`D=[a^2-2a+1-1+3a-a^2-a^2-a-1]/[(-a^2-1)(a^2+a+1)]`
`D=[-a^2-1]/[(-a^2-1)(a^2+a+1)]=1/[a^2+a+1]`
`c)` Với `a ne 1` có:
`1/D=1/[1/[a^2+a+1]]=a^2+a+1=(a+1/2)^2+3/4`
Vì `(a+1/2)^2 >= 0 AA a ne 1`
`=>(a+1/2)^2+3/4 >= 3/4 AA a ne 1`
Hay `1/D >= 3/4 AA a ne 1=>1/D _[mi n]=3/4`
Dấu "`=`" xảy ra `<=>a=-1/2` (t/m).


vì a2> hoặc =0 => áp dụng BDT cauchy ta có:
a2+1/a2> hoặc = 2
=> GTNN của bt = 2 khi và chỉ khi a2=1/a2 <=> a=1

\(a+b=1\Rightarrow a=\dfrac{1}{2}+x;b=\dfrac{1}{2}+y\left(x+y=0\right)\)
có: \(A=a\left(a^2+2b\right)+b\left(b^2-a\right)=a^3+b^3+ab=a^2+b^2\\ =\left(\dfrac{1}{2}+x\right)^2+\left(\dfrac{1}{2}+y\right)^2=\dfrac{1}{2}+x^2+y^2\ge\dfrac{1}{2}\)
\(\Rightarrow A_{min}=\dfrac{1}{2}\Leftrightarrow x=y=0\Leftrightarrow a=b=\dfrac{1}{2}\)
\(a+b=1\)
\(\Rightarrow a^2+2ab+b^2=1\)
\(\Rightarrow\left(a^2+b^2\right)+2ab=1\)
\(\Rightarrow2ab+2ab\le1\) (do \(a^2+b^2\ge2ab\))
\(\Rightarrow ab\le\dfrac{1}{4}\)
\(A=a\left(a^2+2b\right)+b\left(b^2-a\right)\)
\(=a^3+2ab+b^3-ab\)
\(=a^3+b^3+ab\)
\(=\left(a+b\right)^3-3ab\left(a+b\right)+ab\)
\(=1^3-3ab+ab=1-2ab\ge1-2.\dfrac{1}{4}=\dfrac{1}{2}\)
\(A_{min}=\dfrac{1}{2}\Leftrightarrow a=b=\dfrac{1}{2}\)

Điều kiện x ≠ 2 và x ≠ 0
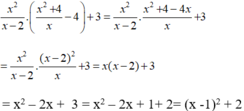
Vì x - 1 2 ≥ 0 nên x - 1 2 + 2 ≥ 2 với mọi giá trị của x.
Khi đó giá trị nhỏ nhất của biểu thức bằng 2 khi x = 1.
Vậy biểu thức đã cho có giá trị nhỏ nhất bằng 2 tại x = 1.