Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

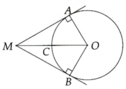
Xét tam giác \(OAM\)vuông tại \(A\):
\(cos\widehat{AOM}=\frac{OA}{OM}=\frac{5}{10}=\frac{1}{2}\Rightarrow\widehat{AOM}=60^o\).
Tương tự \(\widehat{BOM}=60^o\).
\(\widehat{AOB}=\widehat{AOM}+\widehat{BOM}=60^o+60^o=120^o\)

" Đường thẳng MO cắt tâm O tại I và C mà I,C nằm giữa M, O"???
Đoạn này sai sai. Bạn xem lại đề.

Do MA và MB là 2 tiếp tuyến \(\Rightarrow\widehat{OAM}=\widehat{OBM}=90^0\)
Mà tổng 4 góc trong tức giác bằng 360 độ
\(\Rightarrow\widehat{AOB}=360^0-\left(\widehat{OAM}+\widehat{OBM}+\widehat{AMB}\right)=140^0\)
b. Do MA, MB là 2 tiếp tuyến \(\Rightarrow OM\) đồng thời là phân giác \(\widehat{AMB}\)
\(\Rightarrow\widehat{AMO}=\widehat{BMO}=\dfrac{1}{2}\widehat{AMB}\) (1)
Mà ON song song AM (cùng vuông góc OA)
\(\Rightarrow\widehat{AMO}=\widehat{NOM}\) (so le trong) (2)
(1);(2) \(\Rightarrow\widehat{NOM}=\widehat{BMO}\)
\(\Rightarrow\Delta OMN\) cân tại N