Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

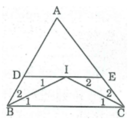
Đường thẳng đi qua I song song với BC cắt AB tại D và AC tại E, ta có các hình thang sau: BDEC, BDIC, BIEC

b) Ta có: \(\widehat{DBI}=\widehat{IBC}\)(gt)
mà \(\widehat{DIB}=\widehat{IBC}\)(hai góc so le trong, DI//BC)
nên \(\widehat{DBI}=\widehat{DIB}\)
hay ΔDIB cân tại D
Ta có: \(\widehat{EIC}=\widehat{ICB}\)(hai góc so le trong, IE//BC)
mà \(\widehat{ECI}=\widehat{ICB}\)(gt)
nên \(\widehat{EIC}=\widehat{ECI}\)
hay ΔEIC cân tại E

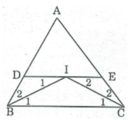
DE // BC (theo cách vẽ)
⇒ ∠ I 1 = ∠ B 1 (hai góc so le trong)
Mà ∠ B 1 = ∠ B 2 (gt)
Suy ra: ∠ I 1 = ∠ B 2
Do đó: ∆ BDI cân tại D ⇒ DI = DB (1)
Ta có: ∠ I 2 = ∠ C 1 (so le trong)
∠ C 1 = ∠ C 2 (gt)
Suy ra: ∠ I 2 = ∠ C 2 do đó: ∆ CEI cân tại E
⇒ IE = EC (2)
DE = DI + IE (3)
Từ (1), (2), (3) suy ra: DE = BD + CE

em tự vẽ hình
câu 1 em tự chứng minh nhé
câu 2,
ta có IE//BC\(\Rightarrow\widehat{EIC}=\widehat{ICB}\) (so le trong)
mà \(\widehat{ECI}=\widehat{ICB}\) (phân giác )
=> \(\widehat{EIC}=\widehat{ECI}\)
=> tam giác IEC cân tại E
chứng minh tương tự cvới tam giác kia nhé
c)
ta có tam giác IEC cân tại E=> IE=EC
vơi tam giác kia cân thì ta có IF=FB
=> IE+IF=BF+CE
=> EF=BF+IC

b: Xét ΔDBI có
\(\widehat{DBI}=\widehat{DIB}\)
nên ΔDBI cân tại D
Xét ΔEIC có \(\widehat{EIC}=\widehat{ECI}\)
nên ΔEIC cân tại E
Ta có: DE=DI+IE
nên DE=DB+EC
Vậy: BDEC là hình thang có một cạnh đáy bằng tổng hai cạnh bên

a: Xét ΔBNQ có
C là trung điểm của BQ
CA//NQ
Do đó: A là trung điểm của NB
Xét ΔCPM có
B là trung điểm của CP
CA//MP
DO đó: A là trung điểm của CM
Xét tứ giác BMNC có
A là trung điểm chung của BN và MC
nên BMNC là hình bình hành
b: Để ANKM là hình bình hành
nên AM//KN và AN//KM
=>AB//MK và AB=MK
=>ABMK là hình bình hành
=>AI//BM
Xét ΔCBM có
A là trung điểm của CA
AI//BM
DO đó; I là trung điểm của BC

a,
Do \(DE||BC\) (gt) \(\Rightarrow BDEC\) là hình thang
Do \(DE||BC\Rightarrow DI||BC\Rightarrow BDIC\) là hình thang
Do \(DE||BC\Rightarrow IE||BC\Rightarrow BIEC\) là hình thang
b.
Do \(DI||BC\Rightarrow\widehat{CBI}=\widehat{BID}\) (so le trong)
Mà \(\widehat{CBI}=\widehat{DBI}\) (do BI là phân giác góc B)
\(\Rightarrow\widehat{DBI}=\widehat{BID}\)
\(\Rightarrow\Delta BDI\) cân tại D
Tương tự ta có \(\widehat{ICB}=\widehat{CIE}\) (so le trong) và \(\widehat{ICB}=\widehat{ICE}\) (do IC là phân giác góc C)
\(\Rightarrow\widehat{CIE}=\widehat{ICE}\Rightarrow\Delta IEC\) cân tại E
c.
Từ câu b, do \(\Delta BDI\) cân \(\Rightarrow DB=DI\)
Do \(\Delta IEC\) cân \(\Rightarrow IE=CE\)
\(\Rightarrow BD+CE=DI+IE=DE\left(đpcm\right)\)