K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
TC
2
15 tháng 9 2021
Vì: a>2 => a=2+m
b>2 => b=2+n (m, n thuộc N*)
=> a+b= (2+m) +(2+n)
a.b= (2+m). (2+n)
= 2(2+n)+ m(2+n)
= 4+ 2n+ 2m+ mn
= 4+ m+ m+ n+ n+ mn
= (4+ m+ n) +(m +n +mn)
= (2+ m) +(2+ n) + (m+ n+ mn) > (2+ m)+ (2+n)
=> a.b > a+b
DB
4
24 tháng 8 2021
x5 = x2
mình nghĩ trong trường hợp này thì x = 0
nha bạn
24 tháng 8 2021
Sửa đề x5 = x2
Ta có :
x5 = x2
=> x5 - x2 = 0
=> x2 . ( x3 - 1 ) = 0
\(\Rightarrow\orbr{\begin{cases}x^2=0\\x^3-1=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x^3=1\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x=1\end{cases}}\)
D
25 tháng 4 2017
Ta có: \(\frac{131313}{565656}=\frac{131313:10101}{565656:10101}=\frac{13}{56}\)
\(\frac{131313}{727272}=\frac{13}{72}\)
\(\frac{131313}{909090}=\frac{13}{90}\)
\(\Rightarrow C=70\left(\frac{13}{56}+\frac{13}{72}+\frac{13}{90}\right)=70\left(\frac{39}{79}\right)=39\)
Vậy C = 39
25 tháng 4 2017
C=70(\(\frac{13}{56}+\frac{13}{72}+\frac{13}{90}\))=70\(\frac{39}{70}\)=39
15 tháng 5 2016
=>B=\(\frac{12.\left(\frac{1}{13}+\frac{1}{1313}+\frac{1}{131}+\frac{1}{1313}\right)}{15.\left(\frac{1}{13}+\frac{1}{1313}+\frac{1}{131}+\frac{1}{1313}\right)}\)
=>B=\(\frac{12}{15}\)
=>B=\(\frac{4}{5}\)
15 tháng 5 2016
B = \(\frac{12.\left(\frac{1}{13}+\frac{1}{1313}+\frac{1}{131}-\frac{1}{1313}\right)}{15.\left(\frac{1}{13}+\frac{1}{131}-\frac{1}{1313}+\frac{1}{1313}\right)}\)
=\(\frac{12.\left(\frac{1}{13}+\frac{1}{131}\right)}{15.\left(\frac{1}{13}+\frac{1}{131}\right)}\)
=\(\frac{12}{15}=\frac{4}{5}\)
Vậy B = 4/5.
VN
7
27 tháng 4 2015
12 bài trung bình chiếm số phần trăm là: 100%-(50%+40%)=10%
Trường có số HS khối 6 là: 12:10%=120(HS)
**** bạn hiền
30 tháng 4 2017
12 bài trung bình chiếm số % :
100 - ( 50 + 40 ) = 10 ( % )
Trường đó có số hs ở khối 6 là :
12 : 10 = 120 ( hs )
Đáp số : 120 hs .
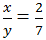
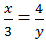
\(S=3+\dfrac{3}{2}+\dfrac{3}{2^2}+...+\dfrac{3}{2^9}\)
\(2S=2\left(3+\dfrac{3}{2}+\dfrac{3}{2^2}+...+\dfrac{3}{2^9}\right)\)
\(2S=6+3+\dfrac{3}{2}+...+\dfrac{3}{2^8}\)
\(2S-S=\left(6+3+...+\dfrac{3}{2^8}\right)-\left(3+\dfrac{3}{2}+...+\dfrac{3}{2^9}\right)\)
\(S=6-\dfrac{3}{2^9}\)
Cái bài tính tổng đó hả?? Trên này mọi người đăng suốt ak!! mk làm hoài ko nhớ ở đâu nữa!
Ta có :
\(S=3+\dfrac{3}{2}+\dfrac{3}{2^2}+\dfrac{3}{2^3}+...................+\dfrac{3}{2^9}\)
\(\Rightarrow2S=2\left(3+\dfrac{3}{2}+\dfrac{3}{2^2}+\dfrac{3}{2^3}+.................+\dfrac{3}{2^9}\right)\)
\(\Rightarrow2S=6+3+\dfrac{3}{2}+\dfrac{3}{2^2}+\dfrac{3}{2^3}+...............+\dfrac{3}{2^8}\)
\(\Rightarrow2S-S=\left(6+3+\dfrac{3}{2}+\dfrac{3}{2^2}+......+\dfrac{3}{2^8}\right)-\left(3+\dfrac{3}{2}+\dfrac{3}{2^2}+........+\dfrac{3}{2^9}\right)\)
\(\Rightarrow S=6-\dfrac{3}{2^9}\)
\(\Rightarrow S=6-\dfrac{3}{512}\)
\(\Rightarrow S=\dfrac{3069}{512}\)