
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tìm số nguyên dương n, biết:
a) 25<5n<625
b)3.27>3nlớn hơn, bằng 9
c)16 bé hơn, bằng 8n bé hơn, bằng 64

a) \(25< 5^n< 625\)
\(25=5^2;625=5^4\)
=> \(5^2< 5^n< 5^4\)
=> 2 < n < 4
=> n = 3
b) \(9\le3^n< 3.27\)
\(9=3^2;3.27=3.3^3=3^4\)
=> \(3^2\le3^n< 3^4\)
=> n = 2; hoặc n = 3
c) \(16\le8^n\le64\)
\(16=8.2;64=8^2\)
=> \(8.2\le8^n\le8^2\)
=> n = 2

Bài 6 :
a) \(\dfrac{625}{5^n}=5\Rightarrow\dfrac{5^4}{5^n}=5\Rightarrow5^{4-n}=5^1\Rightarrow4-n=1\Rightarrow n=3\)
b) \(\dfrac{\left(-3\right)^n}{27}=-9\Rightarrow\dfrac{\left(-3\right)^n}{\left(-3\right)^3}=\left(-3\right)^2\Rightarrow\left(-3\right)^{n-3}=\left(-3\right)^2\Rightarrow n-3=2\Rightarrow n=5\)
c) \(3^n.2^n=36\Rightarrow\left(2.3\right)^n=6^2\Rightarrow\left(6\right)^n=6^2\Rightarrow n=6\)
d) \(25^{2n}:5^n=125^2\Rightarrow\left(5^2\right)^{2n}:5^n=\left(5^3\right)^2\Rightarrow5^{4n}:5^n=5^6\Rightarrow\Rightarrow5^{3n}=5^6\Rightarrow3n=6\Rightarrow n=3\)
Bài 7 :
a) \(3^x+3^{x+2}=9^{17}+27^{12}\)
\(\Rightarrow3^x\left(1+3^2\right)=\left(3^2\right)^{17}+\left(3^3\right)^{12}\)
\(\Rightarrow10.3^x=3^{34}+3^{36}\)
\(\Rightarrow10.3^x=3^{34}\left(1+3^2\right)=10.3^{34}\)
\(\Rightarrow3^x=3^{34}\Rightarrow x=34\)
b) \(5^{x+1}-5^x=100.25^{29}\Rightarrow5^x\left(5-1\right)=4.5^2.\left(5^2\right)^{29}\)
\(\Rightarrow4.5^x=4.25^{2.29+2}=4.5^{60}\)
\(\Rightarrow5^x=5^{60}\Rightarrow x=60\)
c) Bài C bạn xem lại đề
d) \(\dfrac{3}{2.4^x}+\dfrac{5}{3.4^{x+2}}=\dfrac{3}{2.4^8}+\dfrac{5}{3.4^{10}}\)
\(\Rightarrow\dfrac{3}{2.4^x}-\dfrac{3}{2.4^8}+\dfrac{5}{3.4^{x+2}}-\dfrac{5}{3.4^{10}}=0\)
\(\Rightarrow\dfrac{3}{2}\left(\dfrac{1}{4^x}-\dfrac{1}{4^8}\right)+\dfrac{5}{3.4^2}\left(\dfrac{1}{4^x}-\dfrac{1}{4^8}\right)=0\)
\(\Rightarrow\left(\dfrac{1}{4^x}-\dfrac{1}{4^8}\right)\left(\dfrac{3}{2}+\dfrac{5}{3.4^2}\right)=0\)
\(\Rightarrow\dfrac{1}{4^x}-\dfrac{1}{4^8}=0\)
\(\Rightarrow\dfrac{4^8-4^x}{4^{x+8}}=0\Rightarrow4^8-4^x=0\left(4^{x+8}>0\right)\Rightarrow4^x=4^8\Rightarrow x=8\)

| x - 1 | + | x + 3 | = 3 ( * )
xét : x - 1 = 0 => x = 1
x + 3 = 0 => x = -3
x - 1 < 0 => x < 1
x + 3 < 0 => x < -3
x - 1 > 0 => x > 1
x + 3 > 0 => x > -3
Lập bảng xét dấu,ta có :
x -3 1
x+3 - 0 + | +
x-1 - | - 0 +
nếu x < -3 thì * <=> : ( 1 - x ) + ( -3 - x ) = 3
1 - x + ( -3 ) - x = 3
-2x = 5
x = -5/2 ( loại )
nếu -3 \(\le\)x < 1 thì * <=> : ( 1 - x ) + ( x + 3 ) = 3
1 - x + x + 3 = 3
0x = -1 ( ko có GT x thỏa mãn )
nếu x \(\ge\)1 thì * <=> : ( x -1 ) + ( x + 3 ) = 3
x - 1 + x + 3 = 3
2x = 1
x = 1/2 ( ko có GT x thỏa mãn )
Vậy ko có GT x nào thỏa mãn bài trên.
a) 25 < 5n:5 < 625
52 < 5n:5 < 54
2 < n:5 < 4
=> n : 5 = 3
=> n = 15
b) 34 < \(\frac{1}{9}.27^n\)< 310
34 < \(\frac{27^n}{9}\)< 310
34 < 33n-2 < 310
=> 3n - 2 \(\in\) { 5 ; 6 ; 7 ; 8 ; 9 }
Nếu 3n - 2 = 5 thì n = 7/3 ( loại )
Nếu 3n - 2 = 6 thì n = 8/3 ( loại )
Nếu 3n - 2 = 7 thì n = 3 ( thỏa mãn )
Nếu 3n - 2 = 8 thì n = 10/3 ( loại )
Nếu 3n - 2 = 9 thì n = 11/3 ( loại )
Vậy n = 3


\(\frac{25}{5n}\)= 5
=> \(\frac{25}{5n}\)= \(\frac{5}{1}\)
=> 25 = 5 x 5n
=> 25 = 25 x n
=> n = 1
ta có:
\(\frac{25}{5n}=5\)
\(=>\frac{25}{5n}=\frac{5}{1}\)
\(=>25=5.5n\)
\(=>25=25.n\)
\(=>n=25:25\)
\(=>n=1\)
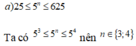
Ta có:\(25< 5^n< 625\)
\(\Leftrightarrow5^2< 5^n< 5^4\)
\(\Leftrightarrow2< x< 4\)
\(\Leftrightarrow x=3\)
Vậy \(x=3\)
25 < 5n < 625
=> 52 < 5n < 54
=> 2 < n < 4
=> n = 3