
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(A=6^2+6^4+6^6+...+6^{98}+6^{100}\)
Ta có: \(A=6^2+6^4+6^6+...+6^{98}+6^{100}\)
\(\Leftrightarrow36A=6^4+6^6+...6^{100}+6^{102}\)
\(\Leftrightarrow A-36A=6^2+6^4+6^6+...6^{98}+6^{100}-6^4-6^6-...-6^{100}-6^{102}\)
\(\Leftrightarrow-35\cdot A=6^2-6^{102}\)
\(\Leftrightarrow A=\dfrac{6^{102}-6^2}{35}\)

Sơ đồ con đường |
Lời giải chi tiết |
|
Ta có: ( 6 100 − 1 ) = ( 6 − 1 ) ( 6 99 + ... + 1 ) = 5 ( 6 99 + ... + 1 ) ⋮ 5 |

a, 6100 - 1 = (6 . 6 . 6 ..... 6) - 1 = [(...6) . (...6) . (...6) ..... (...6)] - 1 = (...6) - 1 = ...5 \(⋮\) 5
b, 2120 - 1110 = (21 . 21 . 21 . 21 . 21..... 21) - (11 . 11 . 11 . 11 ..... 11) = [(...1) . (...1) . (...1) . (...1).....(...1)] - [(...1) . (...1) . (...1) . (...1).....(...1)] = (...1) - (...1) = ....0 \(⋮\) 2; \(⋮\) 5

a/ \(2014^x+80=3^y\)
- Với \(x=0\Rightarrow2014^0+80+3^y\Leftrightarrow81=3^y\Leftrightarrow3^4=3^y\Rightarrow y=4\)
- Với \(x>0\) ta có \(2014\) chẵn \(\Rightarrow2014^x\) chẵn, lại có \(80\) chẵn \(\Rightarrow\) vế trái là một số chẵn
Mà \(3^y\) luôn lẻ với mọi \(y\in N\Rightarrow\) vế phải là số lẻ
Vế trái chẵn, vế phải lẻ \(\Rightarrow\) vô nghiệm
Vậy \(\left\{{}\begin{matrix}x=0\\y=4\end{matrix}\right.\) là cặp nghiệm tự nhiên duy nhất
b/
\(A=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{63}\)
\(A=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{8}+...+\frac{1}{16}+...+\frac{1}{32}+...+\frac{1}{63}\)
\(A< 1+2.\frac{1}{2}+4.\frac{1}{4}+8.\frac{1}{8}+16.\frac{1}{16}+32.\frac{1}{32}\)
\(A< 1+1+1+1+1+1=6\) (đpcm)

a) (-2).(-6)^2+3.(-2)^3
=(-2).36-24=-96
b) (-6).4.(-7).25
=42.100=4200
c) (-85)-105+62
=-190+62=-128
d) 24.(-15)+(-15).75-15
=(-15).(24+75)-15
=(-15).99-15=-1500

a, \(\dfrac{62}{7}.x=\dfrac{29}{90}.\dfrac{3}{56}\)
\(\dfrac{62}{7}.x=\dfrac{29}{1680}\)
\(x=\dfrac{29}{1680}:\dfrac{62}{7}\)
\(x=\dfrac{29}{14880}\)
b, \(\dfrac{1}{5}:x=\dfrac{1}{5}-\dfrac{1}{7}\)
\(\dfrac{1}{5}:x=\dfrac{2}{35}\)
\(x=\dfrac{1}{5}:\dfrac{2}{35}\)
\(x=\dfrac{7}{2}\)
c, \(\left(x+\dfrac{1}{4}-\dfrac{1}{3}\right):\left(2+\dfrac{1}{6}-\dfrac{1}{4}\right)=\dfrac{7}{46}\)
\(\left(x+\dfrac{1}{4}-\dfrac{1}{3}\right):\left(\dfrac{13}{6}-\dfrac{1}{4}\right)=\dfrac{7}{46}\)
\(\left(x+\dfrac{1}{4}-\dfrac{1}{3}\right):\dfrac{23}{12}=\dfrac{7}{46}\)
\(\left(x+\dfrac{-1}{12}\right):\dfrac{23}{12}=\dfrac{7}{46}\)
\(\left(x+\dfrac{-1}{12}\right)=\dfrac{7}{46}.\dfrac{23}{12}\)
\(x+\dfrac{-1}{12}=\dfrac{7}{24}\)
\(x=\dfrac{7}{24}-\dfrac{-1}{12}\)
\(x=\dfrac{3}{8}\)


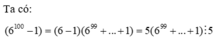
C = 1 + 6 + 62+ 63+...+ 6100
6C = 6 + 62+ 63 +...+ 6100 + 6101
6C - C = 6101 - 1
5C = 6101 - 1
C = \(\dfrac{6^{101}-1}{5}\)
\(C=1+6+6^2+...+6^{100}\)
\(\Rightarrow C=\dfrac{6^{100+1}-1}{6-1}\)
\(\Rightarrow C=\dfrac{6^{101}-1}{5}\)