
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

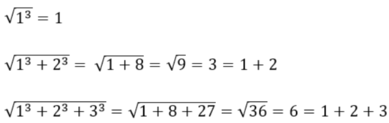

a) Đúng
b) \(\sqrt{1^3+2^3+3^3+4^3}=1+2+3+4\)
\(\sqrt{1^3+2^3+3^3+4^3+5^3=1+2+3+4+5}\)

Các đẳng thức trên luôn đúng:
Ta có công thức tổng quát
\(\sqrt{1^3+2^3+...+n^3}=1+2+..+n\)



a) \(\dfrac{-2}{5}=\dfrac{-14}{35}\)
b) \(\dfrac{9}{4}=\dfrac{\dfrac{1}{4}}{\dfrac{1}{9}}\)

\(VT=2\left|x+3\right|+3\left|x+2\right|+4\left|x+1\right|+5\ge5\) với mọi x
=> VP = \(x\ge5\)
Với \(x\ge5\) ta có: 2(x + 3) + 3(x + 2) + 4(x + 1) + 5 = x
=> 2x + 6 + 3x + 6 + 4x + 4 + 5 = x
=> 9x + 21 = x
=> 9x - x = -21
=> 8x = -21
=> x < 0, không thỏa mãn đk \(x\ge5\)
Vậy không tìm được x thỏa mãn đăng thức như đề bài
Ta có:
\(2\left|x+3\right|+3\left|x+2\right|+4\left|x+1\right|+5=x\)
Ta thấy: \(VT>0\)
Vậy \(x>0\)
Bỏ GTTĐ ta có :
\(8x=-21\)
Vậy x âm (Vô lý)
Không có giá trị của x thỏa mãn.