
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: ĐKXĐ: 2-3x>=0
=>x<=2/3
2: ĐKXĐ: -3x^2>=0
=>x^2<=0
=>x=0
3: ĐKXĐ: -2023x^3>=0
=>x^3<=0
=>x<=0
4: ĐKXĐ: -2(x-5)>=0
=>x-5<=0
=>x<=5
5: ĐKXĐ: -5/2-2x>=0
=>2-2x<0
=>2x>2
=>x>1
6: ĐKXĐ: (x^2+1)(3-2x)>=0
=>3-2x>=0
=>-2x>=-3
=>x<=3/2
7: ĐKXĐ: (-x^2-1)(3-x)>=0
=>(x^2+1)(x-3)>=0
=>x-3>=0
=>x>=3

Bài 4:
b: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
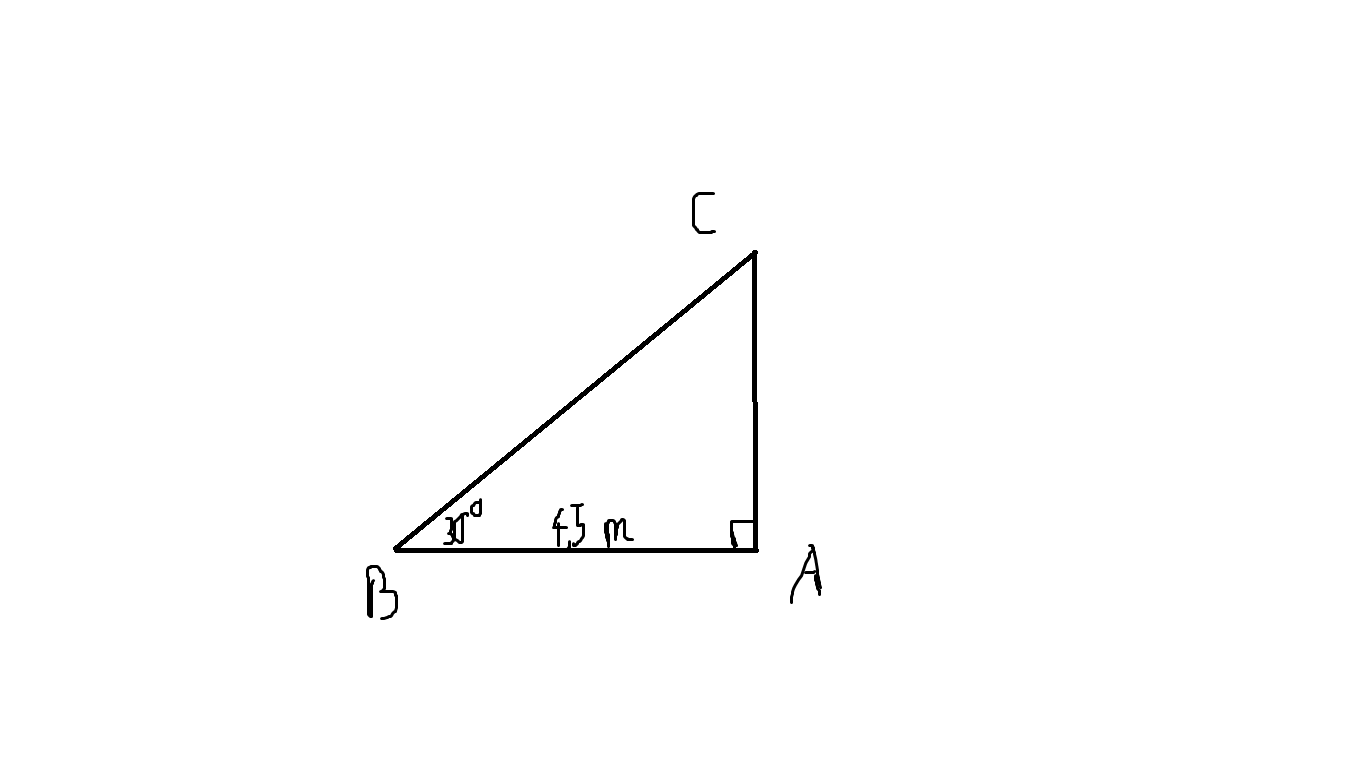
\(TanB=\dfrac{AC}{AB}\Rightarrow Tan30^o=\dfrac{AC}{4,5}\Rightarrow AC=Tan30^o.4,5=\dfrac{3\sqrt{3}}{2}\left(m\right)\)
\(CosB=\dfrac{AB}{BC}\Rightarrow Cos30^o=\dfrac{4,5}{BC}\Rightarrow BC=Cos30^o.4,5=\dfrac{9\sqrt{3}}{4}\)
Chiều cao ban đầu của cây tre là: \(\dfrac{3\sqrt{3}}{2}+\dfrac{9\sqrt{3}}{4}=\dfrac{15\sqrt{3}}{4}\approx6,5\left(m\right)\)

Câu 1:
\(a^2+2ab+b^2-ac-bc\)
\(=\left(a+b\right)^2-c\left(a+b\right)\)
\(=\left(a+b\right)\left(a+b-c\right)\)
Câu 2:
\(5x^2-5y^2-10x+10y\)
\(=5\left(x-y\right)\left(x+y\right)-10\left(x-y\right)\)
\(=\left(x-y\right)\left(5x+5y-10\right)\)
\(=5\left(x-y\right)\left(x+y-2\right)\)
Câu 3:
\(3x^2-6xy+3y^2-12z^2\)
\(=3\left[\left(x-y\right)^2-4z^2\right]\)
\(=3\left(x-y-2z\right)\left(x-y+2z\right)\)
Câu 4:
\(x^4+x^3+x^2-1\)
\(=x^3\left(x+1\right)+\left(x-1\right)\left(x+1\right)\)
\(=\left(x+1\right)\left(x^3+x-1\right)\)
Câu 5:
\(x^3-3x^2+3x-1-y^3\)
\(=\left(x-1\right)^3-y^3\)
\(=\left(x-1-y\right)\left[\left(x-1\right)^2+\left(x-1\right)y+y^2\right]\)
\(=\left(x-y-1\right)\left(x^2-2x+1+xy-y+y^2\right)\)
Câu 6:
\(x^4-x^2+2x-1\)
\(=x^4-\left(x-1\right)^2\)
\(=\left(x^2-x+1\right)\left(x^2+x-1\right)\)
Câu 7:
\(\left(x+y\right)^3-x^3-y^3\)
\(=\left(x+y\right)^3-\left[\left(x+y\right)^3-3xy\left(x+y\right)\right]\)
\(=3xy\left(x+y\right)\)

Câu 2:
\(C=-x+\sqrt{x}\)
\(=-\left(x-\sqrt{x}+\dfrac{1}{4}\right)+\dfrac{1}{4}\)
\(=-\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\le\dfrac{1}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{4}\)


\(1,B=9-5=4\\ 2,\dfrac{\sqrt{5}+1}{3-2\sqrt{2}}-\dfrac{\sqrt{10}}{\sqrt{5}-2}+3\left(\sqrt{2}-\sqrt{5}\right)\\ =\left(\sqrt{5}+1\right)\left(3+2\sqrt{2}\right)-\sqrt{10}\left(\sqrt{5}+2\right)+3\sqrt{2}-3\sqrt{5}\\ =3\sqrt{5}+2\sqrt{10}+3+2\sqrt{2}-5\sqrt{2}-2\sqrt{10}+3\sqrt{2}-3\sqrt{5}=3\)
\(3,\\ a,\left(\dfrac{\sqrt{x}+\sqrt{y}}{1-\sqrt{xy}}+\dfrac{\sqrt{x}+\sqrt{y}}{1+\sqrt{xy}}\right):\left(1+\dfrac{x+y+2xy}{1-xy}\right)\left(x,y\ge0;xy\ne1\right)\\ =\dfrac{\left(\sqrt{x}+\sqrt{y}\right)\left(1+\sqrt{xy}\right)+\left(\sqrt{x}+\sqrt{y}\right)\left(1-\sqrt{xy}\right)}{1-xy}:\dfrac{1-xy+x+y+2xy}{1-xy}\\ =\dfrac{\sqrt{x}+x\sqrt{y}+\sqrt{y}+y\sqrt{x}+\sqrt{x}-x\sqrt{y}+\sqrt{y}-y\sqrt{x}}{1-xy}\cdot\dfrac{1-xy}{1+x+y+xy}\\ =\dfrac{2\left(\sqrt{x}+\sqrt{y}\right)}{\left(1+x\right)+y\left(1+x\right)}=\dfrac{2\left(\sqrt{x}+\sqrt{y}\right)}{\left(1+y\right)\left(1+x\right)}\)
\(b,x=\dfrac{2}{2+\sqrt{3}}=\dfrac{2\left(2-\sqrt{3}\right)}{1}=4-2\sqrt{3}\Leftrightarrow\sqrt{x}=\sqrt{3}-1\)
Thay vào BT
\(=\dfrac{2\left(\sqrt{3}-1+\sqrt{y}\right)}{\left(1+y\right)\left(1+4-2\sqrt{3}\right)}=\dfrac{2\sqrt{3}-2+2\sqrt{y}}{\left(1+y\right)\left(3-2\sqrt{3}\right)}\\ =\dfrac{2\sqrt{3}-2+2\sqrt{y}}{3-2\sqrt{3}+3y-2y\sqrt{3}}\)


1.
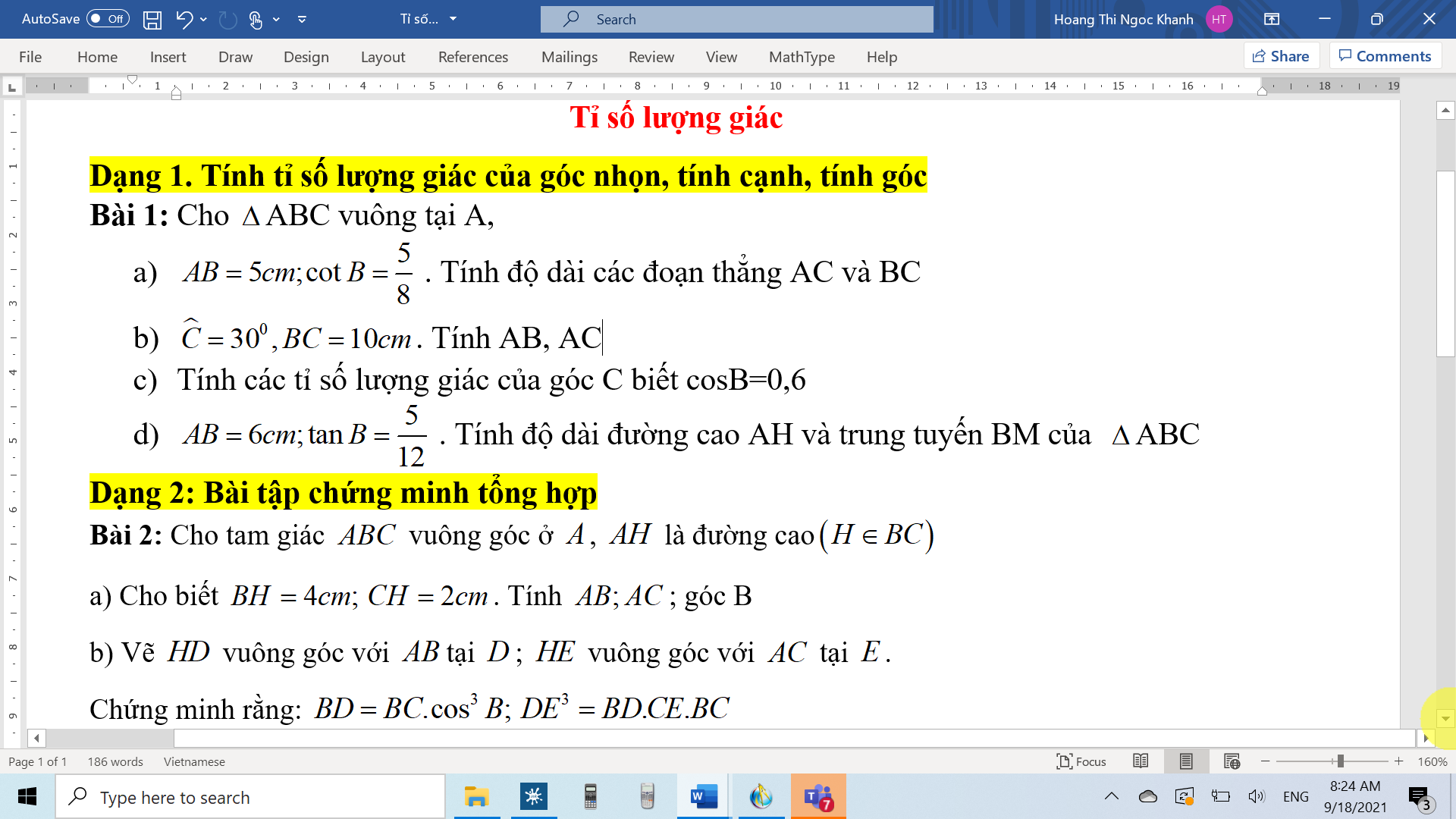
d, ĐK: \(x\ge-5\)
\(x-2-4\sqrt{x+5}=-10\)
\(\Leftrightarrow x+5-4\sqrt{x+5}+3=0\)
\(\Leftrightarrow\left(\sqrt{x+5}-1\right)\left(\sqrt{x+5}-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+5}=1\\\sqrt{x+5}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=1\\x+5=9\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=4\end{matrix}\right.\)
\(\Leftrightarrow x=\pm4\left(tm\right)\)
2.
ĐK: \(x\in R\)
\(\sqrt{x^2+2x+1}+\sqrt{x^2-4x+4}=3\)
\(\Leftrightarrow\sqrt{\left(x+1\right)^2}+\sqrt{\left(x-2\right)^2}=3\)
\(\Leftrightarrow\left|x+1\right|+\left|x-2\right|=3\)
Áp dụng BĐT \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\).
\(\left|x+1\right|+\left|x-2\right|=\left|x+1\right|+\left|2-x\right|\ge\left|x+1+2-x\right|=3\)
Đẳng thức xảy ra khi:
\(\left(x+1\right)\left(2-x\right)\ge0\)
\(\Leftrightarrow-1\le x\le2\)





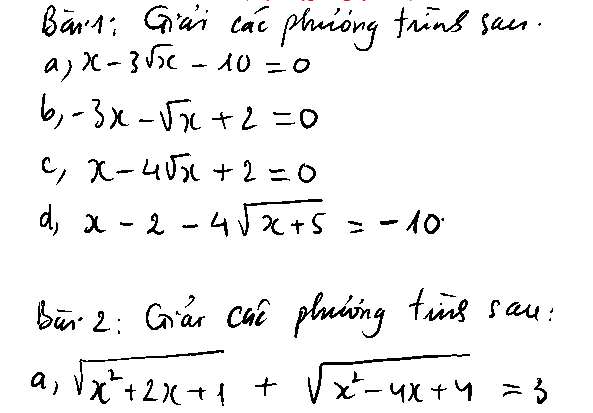
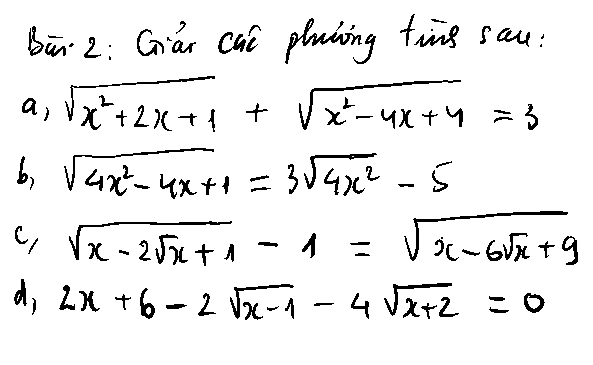
B.(nếu là +)
1.
\(cos^220^o+cos^240^o+cos^250^o+cos^270^o\)
\(=cos^220^o+cos^240^o+sin^240^o+sin^220^o\)
\(=1+1=2\)