K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 8 2021
d: \(\left(\dfrac{1}{2}x-1\right)\left(2x-3\right)\)
\(=x^2-\dfrac{3}{2}x-2x+3\)
\(=x^2-\dfrac{7}{2}x+3\)
e: Ta có: \(\left(x-7\right)\left(x-5\right)\)
\(=x^2-5x-7x+35\)
\(=x^2-12x+35\)
f: Ta có: \(\left(x-\dfrac{1}{2}\right)\left(x+\dfrac{1}{2}\right)\left(4x-1\right)\)
\(=4\left(x-\dfrac{1}{4}\right)\left(x-\dfrac{1}{4}\right)\)
\(=4\left(x-\dfrac{1}{4}\right)^2\)
\(=4\left(x^2-\dfrac{1}{2}x+\dfrac{1}{16}\right)\)
\(=4x^2-2x+\dfrac{1}{4}\)
LT
1
KC
2
14 tháng 10 2021
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
hay ΔABC vuông tại A
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến ứng với cạnh huyền BC
nên \(AM=\dfrac{BC}{2}=\dfrac{10}{2}=5\left(cm\right)\)
TV
4
G
8 tháng 3 2019
\(x^2-4x+y^2-6y+15=2\)
\(\Rightarrow x^2-4x+4+y^2-6y+9+2=2\)
\(\Rightarrow\left(x-2\right)^2+\left(y-3\right)^2=0\Rightarrow\hept{\begin{cases}x=2\\y=3\end{cases}}\)
CT
8 tháng 3 2019
x^2-4x+y^2-6y+15=0
x^2-4x+4+y^2-6y+9+2=2
(x-2)^2+(y-3)^2=0
do x-2)^2>=o, (y-3)^2>= 0( ghi chú : >= là lớn hơn hoặc bằng)
vậy x-2=0 và y-3=0
x=2 và y=3
vậy x=2 và y=3 là nghiệm phương trình
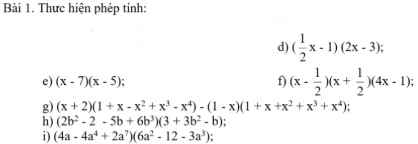
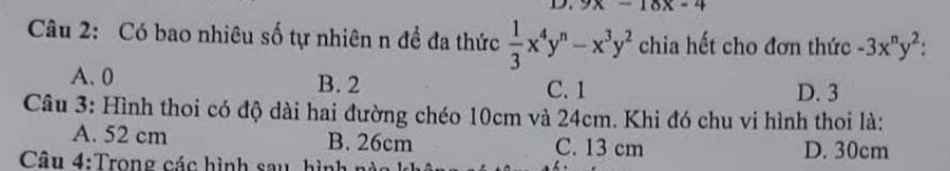
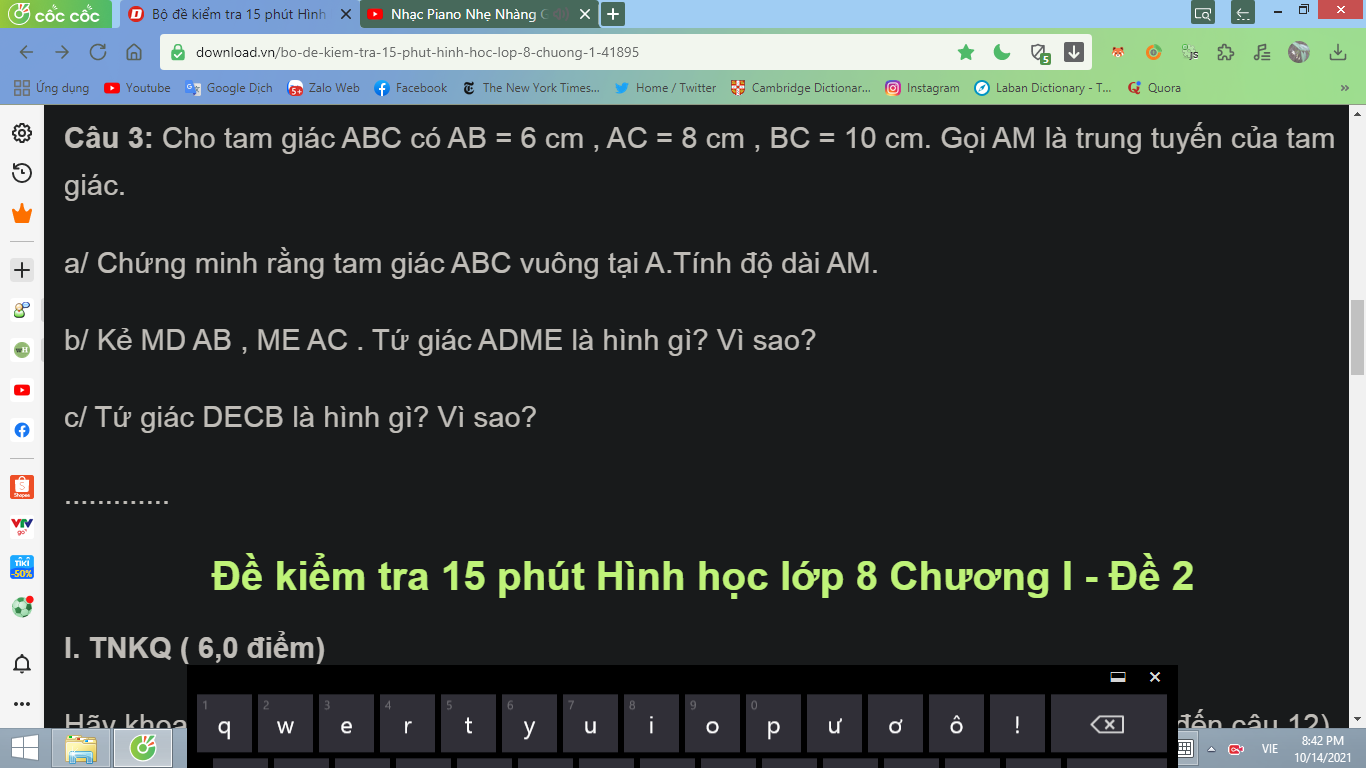
a: \(BC=\sqrt{AB^2+AC^2}=20\left(cm\right)\)
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/12=CD/16
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{12}=\dfrac{CD}{16}=\dfrac{BD+CD}{12+16}=\dfrac{20}{28}=\dfrac{5}{7}\)
Do đó: BD=60/7(cm); CD=80/7(cm)
b: \(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{12\cdot16}{20}=9.6\left(cm\right)\)
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2 = 12 2 + 6 2 = 400
Suy ra: BC =20 (cm)
Vì AD là đường phân giác của ∠(BAC) nên:
\(\dfrac{DB}{DC}=\dfrac{AB}{AC}\) (tính chất đường phân giác)
Suy ra: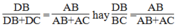
Suy ra: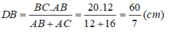
Vậy : DC = BC – DB = 20 - 60/7 = 80/7 (cm)