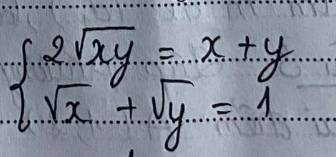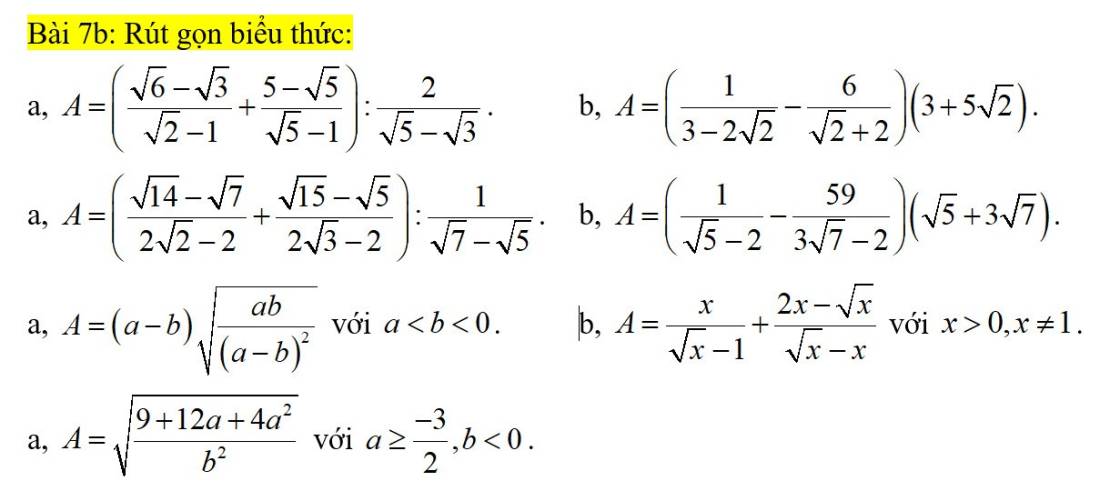3: Xét ΔOHF vuông tại H và ΔOEM vuông tại E có

\(\widehat{HOF}\) chung

Do đó: ΔOHF đồng dạng với ΔOEM

=>\(\dfrac{OH}{OE}=\dfrac{OF}{OM}\)

=>\(OH\cdot OM=OE\cdot OF\)(1)

Xét ΔOAM vuông tại A có AH là đường cao

nên \(OH\cdot OM=OA^2\left(2\right)\)

Từ (1) và (2) suy ra \(OE\cdot OF=OA^2\)

=>\(OE\cdot OF=OC^2\)

=>\(\dfrac{OE}{OC}=\dfrac{OC}{OF}\)

Xét ΔOEC và ΔOCF có

\(\dfrac{OE}{OC}=\dfrac{OC}{OF}\)

\(\widehat{COE}\) chung

Do đó: ΔOEC\(\sim\)ΔOCF

=>\(\widehat{OEC}=\widehat{OCF}=90^0\)

=>CF là tiếp tuyến của (O)

Câu 1:

c. 

PT $(1)\Leftrightarrow x=1+2my$. Thay vô PT $(2)$:
$m(1+2my)+y=2$
$\Leftrightarrow y(2m^2+1)=2-m$

$\Leftrightarrow y=\frac{2-m}{2m^2+1}$

$x=1+2my=1+\frac{4m-2m^2}{2m^2+1}=\frac{4m+1}{2m^2+1}$
Vậy hpt có nghiệm duy nhất $(x,y)=(\frac{4m+1}{2m^2+1}, \frac{2-m}{2m^2+1})$
Để $x,y$ nguyên thì:
$4m+1\vdots 2m^2+1$ và $2-m\vdots 2m^2+1$

$\Rightarrow 4m+1+4(2-m)\vdots 2m^2+1$
$\Leftrightarrow 9\vdots 2m^2+1$

$\Rightarrow 2m^2+1\in\left\{1;3;9\right\}$

$\Rightarrow m\in\left\{0; 1; -1;2;-2\right\}$

Thử lại thì thấy $m=0; -1;2$ thỏa mãn.

Cảm ơn bn nhiều ạ

\(\Leftrightarrow\left\{{}\begin{matrix}\left(\sqrt{x}-\sqrt{y}\right)^2=0\\\sqrt{x}+\sqrt{y}=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}-\sqrt{y}=0\\\sqrt{x}+\sqrt{y}=1\end{matrix}\right.\)

\(\Rightarrow2\sqrt{x}=1\Rightarrow x=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)

\(\Rightarrow y=\dfrac{1}{4}\)

Vậy hệ phương trình có tập nghiệm \(S=\left(\dfrac{1}{4};\dfrac{1}{4}\right)\)

Không ;-;

nếu câu a và b ko liên quan đến hình thì b vẫn dc điểm câu a và b còn nếu nó lq đến hình thì coi như bỏ (vì sai hình ko chấm điểm b nhé)

\(a,\) Áp dụng HTL cho tam giác ABK và ACK:

\(\left\{{}\begin{matrix}AE\cdot AB=AK^2\\AF\cdot AC=AK^2\end{matrix}\right.\Rightarrow AE\cdot AB=AF\cdot AC\)

\(b,AE\cdot AB=AF\cdot AC\Rightarrow\dfrac{AE}{AC}=\dfrac{AF}{AB}\)

Mà có \(\widehat{BAC}\) chung

\(\Rightarrow\Delta AEF\sim\Delta ACB\left(c.g.c\right)\)

\(c,AK=\sqrt{AB^2-BK^2}=12\left(cm\right)\left(pytago\right) \)

Áp dụng HTL tam giác: \(AK^2=AB\cdot AE\Rightarrow AE=\dfrac{AK^2}{AB}=\dfrac{12^2}{13}=\dfrac{144}{13}\left(cm\right)\)

Ta có \(KC=BC-BK=13-5=8\left(cm\right)\)

\(AC=\sqrt{AK^2+KC^2}=\sqrt{12^2+8^2}=4\sqrt{13}\left(cm\right)\left(pytago\right)\)

Vì \(\Delta AEF\sim\Delta ACB\) \(\Rightarrow\dfrac{AE}{AC}=\dfrac{EF}{BC}\Rightarrow EF=\dfrac{AE\cdot BC}{AC}=\dfrac{\dfrac{144}{13}\cdot13}{4\sqrt{13}}=\dfrac{144}{4\sqrt{13}}=\dfrac{36\sqrt{13}}{13}\left(cm\right)\)

\(\dfrac{S_{AEF}}{S_{ABC}}=\left(\dfrac{AE}{AC}\right)^2=\left(\dfrac{\dfrac{144}{13}}{4\sqrt{13}}\right)^2=\left(\dfrac{36\sqrt{13}}{169}\right)^2=\dfrac{16848}{28561}=\dfrac{1296}{2197}\)

\(\dfrac{1}{\sqrt{\dfrac{5}{7}}+\sqrt{\dfrac{5}{13}}+1}+\dfrac{1}{\sqrt{\dfrac{7}{13}}+\sqrt{\dfrac{7}{5}}+1}+\dfrac{1}{\sqrt{1\dfrac{6}{7}}+\sqrt{2\dfrac{3}{5}}+1}\\ =\dfrac{1}{\dfrac{\sqrt{5}}{\sqrt{7}}+\dfrac{\sqrt{5}}{\sqrt{13}}+\dfrac{\sqrt{5}}{\sqrt{5}}}+\dfrac{1}{\dfrac{\sqrt{7}}{\sqrt{13}}+\dfrac{\sqrt{7}}{\sqrt{5}}+\dfrac{\sqrt{7}}{\sqrt{7}}}+\dfrac{1}{\dfrac{\sqrt{13}}{\sqrt{7}}+\dfrac{\sqrt{13}}{\sqrt{5}}+\dfrac{\sqrt{13}}{\sqrt{13}}}\\ =\left(\dfrac{1}{\sqrt{5}}+\dfrac{1}{\sqrt{7}}+\dfrac{1}{\sqrt{13}}\right)\cdot\dfrac{1}{\dfrac{1}{\sqrt{5}}+\dfrac{1}{\sqrt{7}}+\dfrac{1}{\sqrt{13}}}\\ =1\)

Làm giúp mik bài 2 vs 4 với ạ pls

35

\(20\sqrt[]{3}\sim34,64=35\)

a: \(A=\left(\dfrac{\sqrt{6}-\sqrt{3}}{\sqrt{2}-1}+\dfrac{5-\sqrt{5}}{\sqrt{5}-1}\right):\dfrac{2}{\sqrt{5}-\sqrt{3}}\)

\(=\left(\dfrac{\sqrt{3}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}+\dfrac{\sqrt{5}\left(\sqrt{5}-1\right)}{\sqrt{5}-1}\right):\dfrac{2\left(\sqrt{5}+\sqrt{3}\right)}{2}\)

\(=\dfrac{\left(\sqrt{3}+\sqrt{5}\right)}{\sqrt{3}+\sqrt{5}}=1\)

a:

\(A=\left(\dfrac{\sqrt{14}-\sqrt{7}}{2\sqrt{2}-2}+\dfrac{\sqrt{15}-\sqrt{5}}{2\sqrt{3}-2}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)

\(=\left(\dfrac{\sqrt{7}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}+\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{2\left(\sqrt{3}-1\right)}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)

\(=\left(\dfrac{\sqrt{7}+\sqrt{5}}{2}\right)\cdot\dfrac{\sqrt{7}-\sqrt{5}}{1}=\dfrac{7-5}{2}=1\)

a: 

\(A=\left(a-b\right)\cdot\sqrt{\dfrac{ab}{\left(a-b\right)^2}}\)

\(=\left(a-b\right)\cdot\dfrac{\sqrt{ab}}{\left|a-b\right|}\)

a<b<0

=>a-b<0

=>\(A=\left(a-b\right)\cdot\dfrac{\sqrt{ab}}{-\left(a-b\right)}=-\sqrt{ab}\)

a:

\(A=\sqrt{\dfrac{9+12a+4a^2}{b^2}}\)

\(=\sqrt{\dfrac{\left(2a+3\right)^2}{b^2}}=\left|\dfrac{2a+3}{b}\right|\)

a>=-3/2

=>2a+3>=0

b<0

=>\(\dfrac{2a+3}{b}< =0\)

=>\(A=\dfrac{-\left(2a+3\right)}{b}\)

b:

\(A=\left(\dfrac{1}{3-2\sqrt{2}}-\dfrac{6}{2+\sqrt{2}}\right)\left(3+5\sqrt{2}\right)\)

\(=\left(\dfrac{3+2\sqrt{2}}{1}-\dfrac{6\left(2-\sqrt{2}\right)}{2}\right)\left(3+5\sqrt{2}\right)\)

\(=\left(3+2\sqrt{2}-3\left(2-\sqrt{2}\right)\right)\cdot\left(3+5\sqrt{2}\right)\)

\(=\left(5\sqrt{2}-3\right)\left(5\sqrt{2}+3\right)\)

=50-9

=41

b:

\(A=\left(\dfrac{1}{\sqrt{5}-2}-\dfrac{59}{3\sqrt{7}-2}\right)\left(3\sqrt{7}+\sqrt{5}\right)\)

\(=\left(\dfrac{\sqrt{5}+2}{5-4}-\dfrac{59\left(3\sqrt{7}+2\right)}{63-4}\right)\left(3\sqrt{7}+\sqrt{5}\right)\)

\(=\left(\sqrt{5}+2-3\sqrt{7}-2\right)\left(3\sqrt{7}+\sqrt{5}\right)\)

\(=\left(\sqrt{5}-3\sqrt{7}\right)\left(\sqrt{5}+3\sqrt{7}\right)\)

=5-63

=-58

b:

\(A=\dfrac{x}{\sqrt{x}-1}+\dfrac{2x-\sqrt{x}}{\sqrt{x}-x}\)

\(=\dfrac{x}{\sqrt{x}-1}-\dfrac{2x-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\)

\(=\dfrac{x-2\sqrt{x}+1}{\sqrt{x}-1}=\sqrt{x}-1\)