
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đường tròn tâm \(I\left(1;2\right)\)
Gọi B là điểm đối xứng I qua Ox \(\Rightarrow B\left(1;-2\right)\) đồng thời \(IM=BM\)
Áp dụng BĐT tam giác:
\(IM+MA=BM+MA\ge AB\)
Dấu "=" xảy ra khi và chỉ khi M;A;B thẳng hàng hay M là giao điểm của AB và Ox
\(\overrightarrow{BA}=\left(5;4\right)\Rightarrow\) phương trình đường thẳng AB:
\(4\left(x-6\right)-5\left(y-2\right)=0\Leftrightarrow4x-5y-14=0\)
Tọa độ M là nghiệm: \(\left\{{}\begin{matrix}4x-5y-14=0\\y=0\end{matrix}\right.\) \(\Rightarrow M\left(\dfrac{7}{2};0\right)\)

3.
\(A\cap\varnothing=\varnothing\) nên C sai
4.
Tập A có 3 phần tử nên có \(2^3=8\) tập con

Đặt y = f(x) = - 2x2 có đồ thị (C)
và y = g(x) = - 2x2 - 6x + 3 có đồ thị (C')
Ta có :
g(x) = - 2x2 - 6x + 3
= - 2\(\left(x^2+3x-\dfrac{3}{2}\right)\)
= - 2\(\left(x+\dfrac{3}{2}\right)^2\) + \(\dfrac{15}{2}\)
= \(f\left(x+\dfrac{3}{2}\right)+\dfrac{15}{2}\)
Vậy tịnh tiến (C) sang trái \(\dfrac{3}{2}\) đơn vị rồi kéo (C) lên trên \(\dfrac{15}{4}\) đơn vị ta được (C')

Lời giải:
a.
$|x|\leq 2\Leftrightarrow -2\leq x\leq 2$
Tập $A=[-2;2]$
$(x-1)(x-4)< 0\Leftrightarrow 1< x< 4$
Tập $B=(1;4)$
Đến đây bạn có thể dễ dàng biểu diễn nó trên trục số
b.
$A\cap B=[-2;2]\cap (1;4)=(1;2]$
$A\cup B=[-2;2]\cup (1;4)=[-2;4)$
$A\setminus B= [-2;2]\setminus (1;4)=[-2;1]$

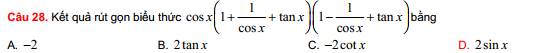

 giải câu c mih cảm ơn ạ
giải câu c mih cảm ơn ạ


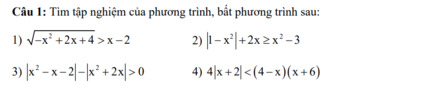
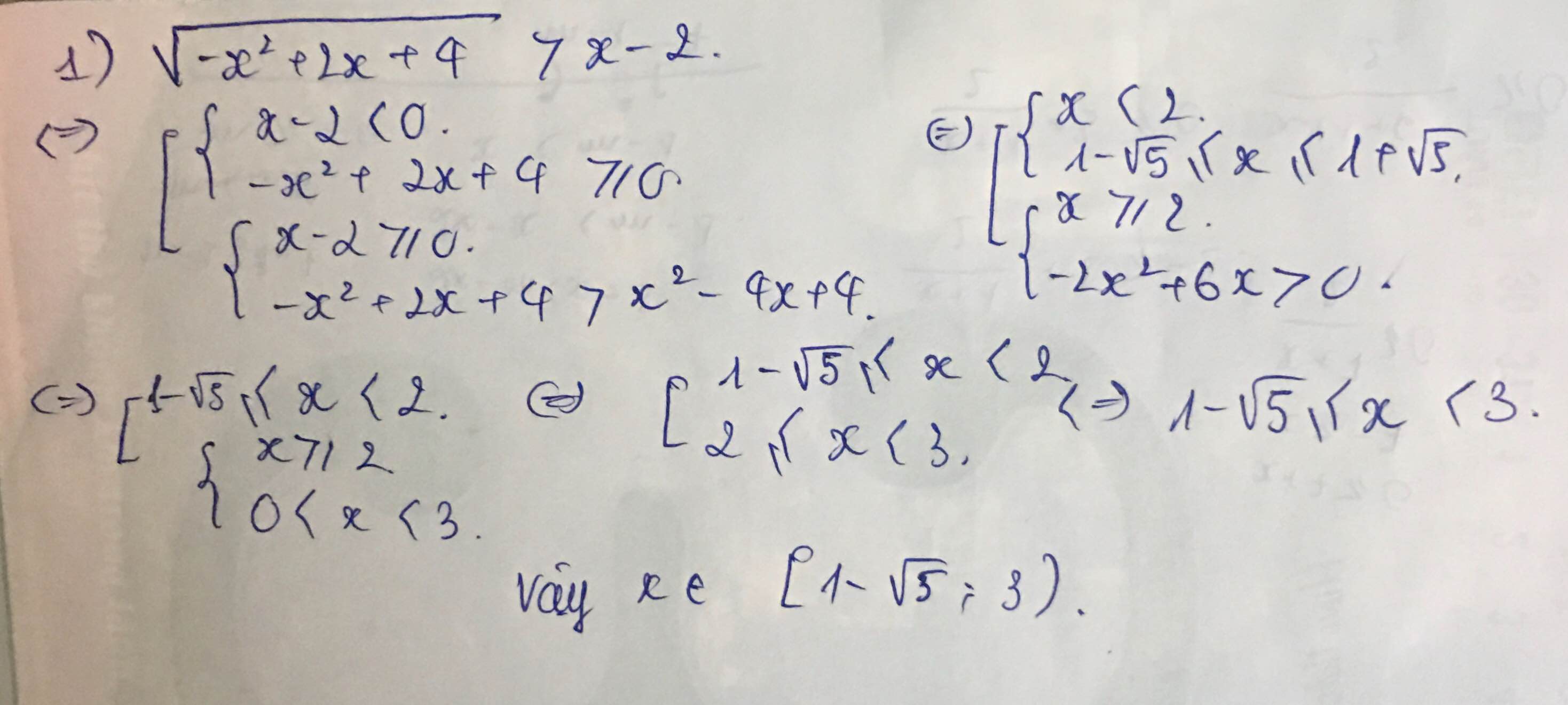


cosx(1 + 1/cosx + tanx)(1 - 1/cosx + tanx)
= cosx[(1 + tanx)² - 1/cos²x]
= cosx(1 + tan²x + 2tanx - 1 - tan²x)
= 2tanxcosx
= 2sinxcosx/cosx
= 2sinx
Chọn D
\(=cosx\left(1+\dfrac{1}{cosx}+\dfrac{sinx}{cosx}\right)\left(1-\dfrac{1}{cosx}+\dfrac{sinx}{cosx}\right)\)
\(=cosx\left(\dfrac{sinx+1+cosx}{cosx}\right)\left(\dfrac{cosx+sinx-1}{cosx}\right)\)
\(=\left(cosx+sinx\right)^2\)\(-1\)
\(=cos^2x+2cosxsinx+sin^2x-1\)
\(=cos^2x+sin^2x+2cosxsinx-1\)
\(=1+2cosxsinx-1\)
\(=2cosxsinx\)
Áp dụng đẳng thức góc nhân đôi cho sin
\(=2sinx\)