Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
Đa thức: \(f\left(x\right)=ax^2+bx+c\) ⋮ 5
\(\Rightarrow f\left(x\right)=5\cdot\left(\dfrac{a}{5}x^2+\dfrac{b}{5}x+\dfrac{c}{5}\right)\) ⋮ 5
\(\Rightarrow a,b,c\in B\left(5\right)\)
Vậy khi f(x) chia hết cho 5 thì a,b,c chia hết cho 5
f=84[05\66\ơ515[52[ư4[\
7;ơ4411[ư1[5
4
4['\
vì
ik
k\uyke]
'uy
'^k''m '\7ys'tfdh'se\ử'ý'0rtư

Cho đa thức f(x)=ax2+bx+c với a,b,c là các số hữu tỉ thỏa mãn 2a-b=0
CMR: f(-5)×f(3) ko thể là số âm.


\(a.f\left(1\right)=f\left(-1\right)\Leftrightarrow a+b+c=a-b+c\Leftrightarrow2b=0\Leftrightarrow b=0\)
\(\Rightarrow f\left(x\right)=ax^2+c\)
Khi đó ta có:
\(\left\{{}\begin{matrix}f\left(m\right)=am^2+c\\f\left(-m\right)=am^2+c\end{matrix}\right.\Rightarrow f\left(m\right)=f\left(-m\right)\forall m\)
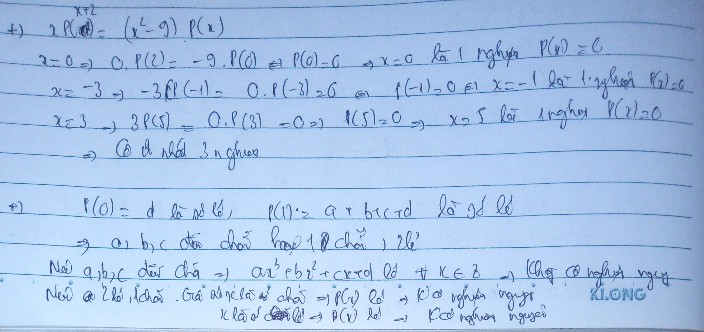
Thay A, B, C vào biểu thức ta được:
\(Ax^2+Bx+C\)
\(=8x^5y^3.x^2+\left(-2x^6y^3.x\right)-6x^7y^3\)
\(=8x^7y^3-2x^7y^3-6x^7y^3\)
\(=\left(8-2-6\right)x^7y^3\)
\(=0\)
=> ĐPCM
thanks vì đã giúp đỡ mình