Đáp án B

(C) có I(6 ; 2), bán kính 1

Đường thẳng đi qua I và vuông góc với (d) có vectơ pháp tuyến

 Phương trình đường thẳng :   ( x – 6 ) –  ( y – 2 ) = 0

x –  y – 4 = 0

Δ ∩ d =>  O 5 2 ; − 3 2

Đ 0  : I -> I’(–1 ; –5 )

Phương  trình đường tròn (C’):   x + 1 2 + y + 5 2 = 1

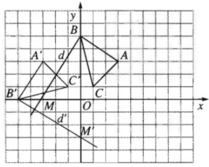
a) Lấy hai điểm A(0;4) và B(2;0) thuộc d. Gọi A′, B′ theo thứ tự là ảnh của A và B qua phép vị tự tâm O tỉ số k = 3. Khi đó ta có

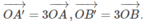
Vì  O A →   =   ( 0 ; 4 ) nên  O A ' →   =   ( 0 ; 12 ) . Do đó A′ = (0;12).

Tương tự B′ = (6;0); d1 chính là đường thẳng A'B' nên nó có phương trình:

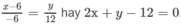
b) Có thể giải tương tự như câu a) .

Sau đây ta sẽ giải bằng cách khác.

Vì d 2   / /   d nên phương trình của d 2  có dạng 2x + y + C = 0.

Gọi A′ = (x′;y′) là ảnh của A qua phép vị tự đó thì ta có:

I A ' →   =   − 2 I A →  hay x′ + 1 = −2, y′ − 2 = −4

Suy ra x′ = −3, y′ = −2

Do A' thuộc d 2  nên 2.(−3) – 2 + C = 0.

Từ đó suy ra C = 8

Phương trình của d 2  là 2x + y + 8 = 0

a) d 1 : 3x + 2y + 6 = 0

b) Giao của d và Δ là A(2;0). Lấy B(0; −3) thuộc d. Ảnh của B qua phép đối xứng của đường thẳng Δ là B′(5;2). Khi đó d' chính là đường thẳng AB′: 2x − 3y – 4 = 0

\(\overrightarrow{AB}\left(7;3\right)\) là 1 vecto chỉ phương của đt 

=> gọi \(\overrightarrow{n}\left(-3;7\right)\) là vecto pháp tuyến của đt

Đt đi qua A(-3;2)

=> pt tổng quát của đt : \(-3\left(x+3\right)+7\left(y-2\right)=0\Leftrightarrow-3x+7y-23=0\)

Đáp án A

Đường thẳng đi qua A và vuông góc với d:  3 ( x − 3 ) − ( y + 2 ) = 0

Δ : 3 x − y − 11 = 0

  Δ ∩ d = M ( 7 2 ; − 1 2 ) ⇔ A’(4;1)

Tương tự  ⇔ B ' − 1 5 ; − 48 5   ⇒ A ' B ' = 130

\(d_2\) vuông góc \(d_1\) nên nhận (1;2) là 1 vtpt

d' là ảnh của \(d_2\) qua phép tịnh tiến \(\Rightarrow d'\) cùng phương \(d_2\Rightarrow d'\) cũng nhận (1;2) là 1 vtpt, pt d' có dạng:

\(x+2y+c=0\) (1)

Gọi A' là ảnh của A qua phép tịnh tiến \(\overrightarrow{v}\Rightarrow A'\in d'\)

\(\left\{{}\begin{matrix}x'=-1+4=3\\y'=2+\left(-3\right)=-1\end{matrix}\right.\) \(\Rightarrow A'\left(3;-1\right)\)

Thế vào (1):

\(3+2.\left(-1\right)+c=0\Rightarrow c=-1\)

Vậy pt d' là: \(x+2y-1=0\)