
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng BĐT Cauchy cho 2 số không âm:
\(4a^2+9b^2\ge2\sqrt{4a^2.9b^2}=2.6ab=12ab\)
\(9b^2+25c^2\ge2\sqrt{9b^2.25c^2}=2.15bc=30bc\)
\(4a^2+25c^2\ge2\sqrt{4a^2.25c^2}=2.10ac=20ac\)
Cộng từng vế của các BĐT trên:
\(2\left(4a^2+9b^2+25c^2\right)\ge2\left(6ab+10ac+15bc\right)\)
\(\Rightarrow4a^2+9b^2+25c^2\ge6ab+10ac+15bc\)
(Dấu "="\(\Leftrightarrow a=b=c=0\))
\(\text{BĐT}\Leftrightarrow\frac{\left(4a-3b-5c\right)^2+3\left(3b-5c\right)^2}{4}\ge0\) (đúng)
Đẳng thức xảy ra khi \(\hept{\begin{cases}4a=3b+5c\\3b=5c\end{cases}}\Leftrightarrow\hept{\begin{cases}4a=6b\\4a=10c\end{cases}}\Leftrightarrow a=\frac{3}{2}b=\frac{5}{2}c\)
Không chắc chỗ dấu bằng cho lắm:)

Bđt cần CM tương đương với:
\(\left(\sqrt{a^2+15bc}+\sqrt{b^2+15ca}+\sqrt{c^2+15ab}\right)^2\le3\left[a^2+b^2+c^2+15\left(ab+bc+ca\right)\right]\)
Ta cần cm \(3\left[a^2+b^2+c^2+15\left(ab+bc+ca\right)\right]\le16\left(a+b+c\right)^2\)
Rút gọn ta đc \(ab+bc+ca\le a^2+b^2+c^2\)
Bđt sau cùng đúng
Ta đc đpcm

Áp dụng bất đẳng thức Cauchy - Schwarz ta có:
\(\left(4a^2+9b^2\right)\left(2^2+2^2\right)\ge\left(2a.1-3b.2\right)^2=\left(4a-6b\right)^2=1\)
\(\Rightarrow4a^2+9b^2\ge\dfrac{1}{8}\).
Đẳng thức xảy ra khi \(a=\dfrac{1}{8};b=\dfrac{-1}{12}\).

\(4a^2+9b^2\ge12ab\)
\(\left(2a\right)^2+\left(3b\right)^2-12ab\ge0\)
\(\left(2a\right)^2-2\cdot2a\cdot3b+\left(3b\right)^2\ge0\)
\(\left(2a-3b\right)^2\ge0\left(đpcm\right)\)
ta có: 4a2 + 9b2 - 12ab = (2a)2 - 2.2a.3b + (3b)2 = ( 2a-3b)2
mà \(\left(2a-3b\right)^2\ge0\)
\(\Rightarrow4a^2+9b^2-12ab\ge0\Rightarrow4a^2+9b^2\ge12ab\)

4a2+9b2+16c2=4a+6b+8c+3 <=>4a2-4a+1+9b2-6b+1+16c2-8c+1=6 <=> (2a-1)2+(3b-1)2+(4c-1)2=6. hướng dẫn đến đây nhe bạn

a) \(a^2+2a+1-b^2\)
\(=\left(a+1\right)^2-b^2\)
\(=\left(a+1-b\right)\left(a+1+b\right)\)
b) \(4a^2+4a+1-9b^2\)
\(=\left(2a\right)^2+4a+1-\left(3b\right)^2\)
\(=\left(2a+1\right)^2-\left(3b\right)^2\)
\(=\left(2a+1-3b\right)\left(2a+1+3b\right)\)

\(a.2a+4b+\left(-4b+5a\right)-\left(6a-9b\right)\)
\(=2a+4b-4b+5a-6a+9b\)
\(=\left(2a+5a-6a\right)+\left(4b-4b+9b\right)\)
\(=a+9b\)
\(b.6a\left[b+3a-\left(4a-b\right)\right]\)
\(=6a\left[b+3a-4a+b\right]\)
\(=6a\left[4a-a+b+b\right]\)
\(=6a\left(3a-2b\right)\)

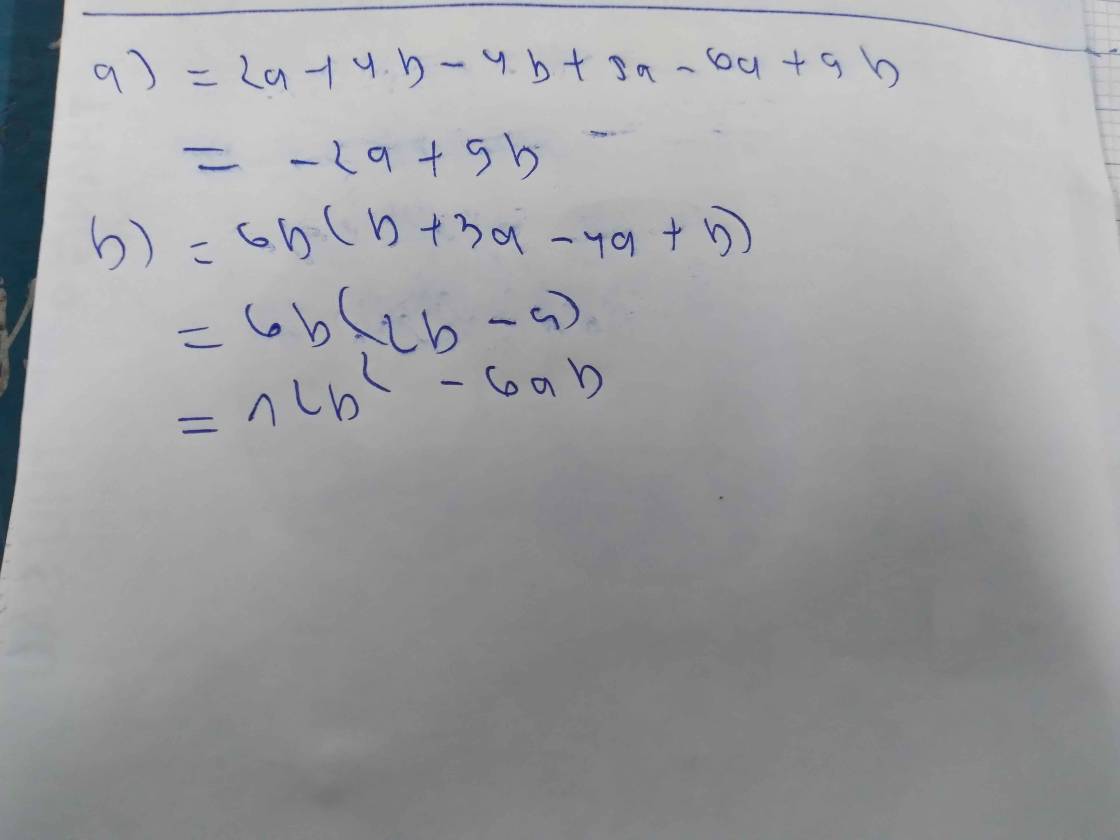
Không biết ông tth SOS như thế nào nhưng mik thì đơn giản thôi ( không có ý định cà khịa nhé người anh em )
Đặt \(x=2a;y=3b;z=5c\)
Khi đó:BĐT cần chứng minh tương đương với:
\(x^2+y^2+z^2\ge xy+yz+zx\)
\(\Leftrightarrow\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge0\) ( đúng )
=> ĐPCM
mình đăng câu hỏi này zì đã đọc cuộc cãi lộn giữa các ctv thôi
haha