Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Sử dụng kết quả sau: Với \(n\in\mathbb{N}\Rightarrow n^5-n\vdots 30\)
Chứng minh:
Ta có: \(n^5-n=n(n^4-1)=n(n-1)(n+1)(n^2+1)\)
Xét thấy \(n-1,n\) là hai số nguyên liên tiếp nên \(n(n-1)\vdots 2\)
\(\Rightarrow n^5-n\vdots 2(1)\)
Xét thấy \(n-1,n,n+1\) là ba số nguyên liên tiếp nên
\(n(n-1)(n+1)\vdots 3\)
\(\Rightarrow n^5-n\vdots 3(2)\)
Xét modulo của 5 cho $n$ :
+) \(n=5k\Rightarrow n^5-n=(5k)^2-(5k)\vdots 5\)
+) \(n=5k+1\Rightarrow n-1=5k\vdots 5\Rightarrow n^5-n\vdots 5\)
+) \(n=5k+2\Rightarrow n^2+1=(5k+2)^2+1=5(5k^2+4k+1)\vdots 5\)
\(\Rightarrow n^5-n\vdots 5\)
+) \(n=5k+3\Rightarrow n^2+1=(5k+3)^2+1=5(5k^2+6k+2)\vdots 5\)
\(\Rightarrow n^5-n\vdots 5\)
+) \(n=5k+4\Rightarrow n+1=5k+5\vdots 5\)
\(\Rightarrow n^5-n\vdots 5\)
Tóm lại trong mọi TH thì \(n^5-n\vdots 5(3)\)
Từ (1);(2);(3) và (2,3,5) là 3 số đôi một nguyên tố cùng nhau nên:
\(n^5-n\vdots (2.3.5=30)\)
--------------------------------
Quay trở tại bài toán. Áp dụng kết quả trên:
\(M-N=(a_1^5-a_1)+(a_2^5-a_2)+...+(a_{2017}^5-a_{2017})\vdots 30\)
Mà \(N\vdots 30\Rightarrow M\vdots 30\)
Vậy ta có đpcm.

Với 0 < a < 1 ta có:
P = 1 + a 1 + a − 1 − a + 1 − a 2 1 − a 1 + a − 1 − a 2 1 − a 2 a 2 − 1 a = 1 + a 1 + a − 1 − a + 1 − a 2 1 − a 1 + a − 1 − a ( 1 − a ) ( 1 + a ) a 2 − 1 a = 1 + a 1 + a − 1 − a + 1 − a 1 + a − 1 − a 1 − a . 1 + a a 2 − 1 a = 1 + a + 1 − a 1 + a − 1 − a . 2 1 − a . 1 + a − ( 1 − a ) − ( 1 + a ) 2 a = 1 + a + 1 − a 1 + a − 1 − a . − 1 + a − 1 − a 2 2 a = − 1 + a + 1 − a 1 + a − 1 − a 2 a = − 1 + a − 1 + a 2 a = − 2 a 2 a = − 1

2:
a: =>a^2+2ab+b^2-2a^2-2b^2<=0
=>-(a^2-2ab+b^2)<=0
=>(a-b)^2>=0(luôn đúng)
b; =>a^2+b^2+c^2+2ab+2ac+2bc-3a^2-3b^2-3c^2<=0
=>-(2a^2+2b^2+2c^2-2ab-2ac-2bc)<=0
=>(a-b)^2+(b-c)^2+(a-c)^2>=0(luôn đúng)
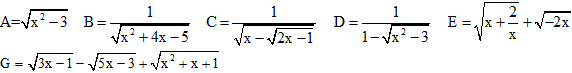 Mn giúp em với ;-;
Mn giúp em với ;-;