Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(f\left(x\right)=x^2-\left(m-1\right)x+3m-2\)
Để đa thức f(x) có nghiệm là -1 khi:
\(f\left(-1\right)=\left(-1\right)^2-\left(m-1\right).\left(-1\right)+3m-2=0\)
\(\Rightarrow1+m-1+3m-2=0\)
\(\Rightarrow4m=2\Rightarrow m=\dfrac{1}{2}\)
b) \(g\left(x\right)=x^2-2\left(m+1\right)x-5m+1\)
Để đa thức g(x) có nghiệm là 2 khi:
\(g\left(2\right)=2^2-2\left(m+1\right).2-5m+1=0\)
\(\Rightarrow4-4\left(m+1\right)-5m+1=0\)
\(\Rightarrow4-4m-1-5m+1=0\)
\(\Rightarrow-9m=-4\Rightarrow m=\dfrac{4}{9}\)
c) \(h\left(x\right)=-2x^2+mx-7m+3\)
Để đa thức h(x) có nghiệm là -1 khi:
\(h\left(-1\right)=-2\left(-1\right)^2+m.\left(-1\right)-7m+3=0\)
\(\Rightarrow-2-m-7m+3=0\)
\(\Rightarrow-8m=-1\Rightarrow m=\dfrac{1}{8}\)
d) -Để \(f\left(1\right)=g\left(2\right)\) khi và chỉ khi
\(1^2-\left(m-1\right).1+3m-2=2^2-2\left(m+1\right).2-5m+1\)
\(\Rightarrow1-m+1+3m-2=4-4m-4-5m+1\)
\(\Rightarrow11m=1\Rightarrow m=\dfrac{1}{11}\)
-Để \(g\left(1\right)=h\left(-2\right)\) khi và chỉ khi
\(1^2-2\left(m+1\right).1-5m+1=-2\left(-2\right)^2+m.\left(-2\right)-7m+3\)
\(\Rightarrow1-2m-2-5m+1=-8-2m-7m+3\)
\(\Rightarrow2m=-5\Rightarrow m=-\dfrac{5}{2}\)

F(x)=0
=>x=-2 hoặc x=1
Để F(x) và G(x) có chung tập nghiệm thì:
-2+4a-2b+2=0 và 1+a+b+2=0
=>4a-2b=0 và a+b=-3
=>a=-1 và b=-2

`f(x) = (x-1)(x+2) = 0`.
`=>` \(\left[ \begin{array}{l}x=1\\x=-2\end{array} \right.\)
Với `x = 1 => g(x) = 1 + a + b + 2 = 0`.
`<=> a + b = -3`.
Với `x = -2 => g(x) = -8 + 4a - 2b + 2 = 0`.
`<=> 4a - 2b = 6`.
`<=> 2a - b = 6`.
`=> ( a + b) + (2a - b) = -3 + 6`.
`=> 3a = 3`.
`=> a = 1.`
`=> b = -4`.
Vậy `(a,b) = {(1, -4)}`.

Chọn A
Ta có f(x) = 0 ⇒ 3x + 4 = 0 ⇒ x = -4/3 ⇒ a = -4/3
g(x) = 0 ⇒ -4x - 5 = 0 ⇒ x = -5/4 ⇒ b = -5/4
Vì -4/3 < -5/4 nên a < b.
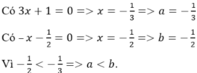
Vì x 2 ≥ 0 ⇒ x 2 + 5 ≥ 5 > 0
Do đó đa thức G ( x ) = x 2 + 5 không có nghiệm.
Chọn đáp án A