Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Ta có: f(x) + h(x) = g(x)
Suy ra: h(x) = g(x) – f(x) = (x4 – x3 + x2 + 5) – (x4 – 3x2 + x – 1)
= x4 – x3 + x2 + 5 – x4 + 3x2 – x + 1
= -x3 + 4x2 – x + 6
b. Ta có: f(x) – h(x) = g(x)
Suy ra: h(x) = f(x) – g(x) = (x4 – 3x2 + x – 1) – (x4 – x3 + x2 + 5)
= x4 – 3x2 + x – 1 – x4 + x3 – x2 – 5
= x3 – 4x2 + x – 6

Bài 3:
\(x=1-\sqrt{2}\Leftrightarrow x^2=3-2\sqrt{2}=2-2\sqrt{2}+1\\ \Leftrightarrow x^2=2x+1\Leftrightarrow x^2-2x-1=0\\ \Leftrightarrow P\left(x\right)=ax^2+bx+c=x^2-2x-1\\ \Leftrightarrow a=1;b=-2;c=-1\\ \Leftrightarrow11a+3b+2x=11-6-2=3⋮3\)

Lời giải:
Không mất tổng quát, giả sử n chẵn.
Khi đó các hệ số bậc chẵn là: \(a_n, a_{n-2},...,a_0\), và các hệ số bậc lẻ là \(a_{n-1}, a_{n-3},...,a_1\). Theo bài ra ta có:
\(a_n+a_{n-2}+...+a_0=a_{n-1}+a_{n-3}+...+a_1(*)\)
Ta thấy \((-1)^k=\left\{\begin{matrix} \text{1 nếu k chẵn}\\ \text{-1 nếu k lẻ}\end{matrix}\right.\). Do đó:
\(F(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0x^0\)
\(\Rightarrow F(-1)=a_n(-1)^n+a_{n-1}(-1)^{n-1}+...+a_1(-1)+a_0\)
\(=a_n+(-1)a_{n-1}+a_{n-2}+(-1)a_{n-3}+....+(-1)a_1+a_0\)
\(=(a_n+a_{n-2}+...+a_0)-(a_{n-1}+a_{n-3}+...+a_1)\)
\(=0\) (do $(*)$)
Vậy \(F(-1)=0\), tức là $x=-1$ là nghiệm của đa thức $F(x)$

a,f(x)+g(x)=\(\left(a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\right)+\left(b_nx^{n-1}+...+b_1x+b_0\right)\)
=\(a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0+b_nx^n+b_{n-1}x^{n-1+...+b_1x+b_0}\)
\(=\left(a_nx^n+b_nx^n\right)+\left(a_{n-1}x^{n-1}+b_{n-1}x^{n-1}\right)+...+\left(a_1x+b_1x\right)+\left(a_0+b_0\right)\)
b
f(x)+g(x)=\(\left(a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\right)+\left(b_nx^n+b_{n-1}x^{n-1}+...+b_1x+b_0\right)\)
\(=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0-b_nx^n-b_{n-1}-b_1x+b_0\)
\(=(a_nx^n-b_nx^n)+(a_{n-1}x^{n-1}-b_{n-1}x^{n-1})+...+(a_1x-b_1x)+\left(a_0+b_0\right)\)
\(=\left(a_n-b_n\right)x^n+(a_{n-1}-b_{n-1})x^{n-1}+...+\left(a_1-b_1\right)x+\left(a_0-b_0\right)\)
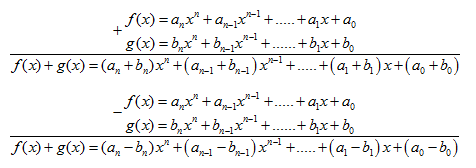
Gỉa sử P(x) có một nghiệm nguyên là \(x_0\left(x_0\ne0\right)\)
Ta có \(P\left(x\right)=a_nx_0^n+a_{n-1}x_0^{n-1}+...+a_1x_0+a_0=0.\)
Như vậy \(P\left(x_0\right)=0⋮x_0\)và các số hạng \(a_nx_0^n+a_{n-1}x_0^{n-1}+...+a_1x_0\)đều chia hết cho \(x_0\), suy ra \(a_0\)cũng phải chia hết \(x_0\)tức \(x_0\)là ước của \(a_0\)