Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tham khảo cách làm của bạn Thư Vy nhé :
Câu hỏi của George H. Dalton - Toán lớp 7 | Học trực tuyến
\(\frac{cy-bz}{x}=\frac{az-cx}{y}=\frac{bx-ay}{z}=\frac{xyc-bxz}{x^2}=\frac{ayz-xyc}{y^2}=\frac{xzb-ayz}{z^2}\)
\(=\frac{cxy-bxz+ayz-cxy+bxz-ayz}{x^2+y^2+z^2}=0\) ( theo t/c dãy tỉ số bằng nhau )
\(\Rightarrow\left\{{}\begin{matrix}cy=bz\\az=cx\\bx=ay\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\frac{c}{z}=\frac{b}{y}\\\frac{a}{x}=\frac{c}{z}\\\frac{b}{y}=\frac{a}{x}\end{matrix}\right.\Rightarrow\frac{a}{x}=\frac{b}{y}=\frac{c}{z}\)

\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{ax}{cx}=\dfrac{yb}{yd}=\dfrac{ax+yb}{cx+yd}\) (1)
Tương tự: \(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{za}{zc}=\dfrac{tb}{td}=\dfrac{za+tb}{zc+td}\) (2)
(1);(2) \(\Rightarrow\dfrac{ax+yb}{cx+yd}=\dfrac{za+tb}{zc+td}\Rightarrow\dfrac{xa+yb}{za+tb}=\dfrac{xc+yd}{zc+td}\)
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{xa}{xc}=\dfrac{yb}{yd}=\dfrac{za}{zc}=\dfrac{tb}{td}=\dfrac{xa+yb}{xc+yd}=\dfrac{za+tb}{zc+td}\\ \Rightarrow\dfrac{xa+yb}{za+tb}=\dfrac{xc+yd}{zc+td}\)


Lời giải:
Sửa đề: $z$ đầu tiên ở mẫu đổi thành $a$.
Ta có:
$\frac{bz-cy}{a}=\frac{cx-az}{b}=\frac{ay-bx}{c}$
$=\frac{abz-cya}{a^2}=\frac{bcx-abz}{b^2}=\frac{acy-bcx}{c^2}$
$=\frac{abz-cya+bcx-abz+acy-bcx}{a^2+b^2+c^2}=\frac{0}{a^2+b^2+c^2}=0$
$\Rightarrow bz-cy=cx-az=ay-bx=0$
$\Rightarrow bz=cy; cx=az; ay=bx$
$\Rightarrow \frac{x}{a}=\frac{y}{b}=\frac{z}{c}$
Ta có đpcm.

Ta có :
\(\dfrac{cy-bz}{x}=\dfrac{az-cx}{y}=\dfrac{bx-ay}{z}=\dfrac{bxz-cxy+cxy-ayz+ayz-bxz}{ax+by+cz}=0\)
\(\Rightarrow\dfrac{cy-bz}{x}=0\Rightarrow cy=bz\Rightarrow\dfrac{b}{y}=\dfrac{c}{z}\left(1\right)\)
\(\Rightarrow\dfrac{az-cx}{y}=0\Rightarrow az=cx\Rightarrow\dfrac{a}{x}=\dfrac{c}{z}\left(2\right)\)
Từ (1) và (2) suy ra:\(\dfrac{a}{x}=\dfrac{b}{y}=\dfrac{c}{z}\)

Đặt \(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}=k\) thì \(x=ak,y=bk,z=ck\)
\(\dfrac{bz-cy}{a}=\dfrac{bck-bck}{a}=0\) __( 1 )__
\(\dfrac{cx-az}{b}=\dfrac{ack-ack}{b}=0\) __( 2 )__
\(\dfrac{ay-bx}{c}=\dfrac{abk-abk}{c}=0\) __( 3 )__
Từ ( 1 ), ( 2 ), ( 3 ) suy ra \(\dfrac{bz-cy}{a}=\dfrac{cx-az}{b}=\dfrac{ay-bx}{c}\)

Ta có :
\(\dfrac{cy-bx}{x}=\dfrac{az-cx}{y}=\dfrac{bx-ay}{z}=\dfrac{bxz-cxy+cxy-ayz+ayz-bxz}{ax+by+cz}=0\)
\(\Rightarrow\dfrac{cy-bz}{x}=0\) \(\Rightarrow cy=bz\) \(\Rightarrow\) \(\dfrac{b}{y}=\dfrac{c}{z}\left(1\right)\)
\(\Rightarrow\dfrac{az-cx}{y}=0\) \(\Rightarrow az=cx\) \(\Rightarrow\dfrac{a}{x}=\dfrac{c}{z}\left(2\right)\)
Từ (1) và (2) suy ra : \(\dfrac{a}{x}=\dfrac{b}{y}=\dfrac{c}{z}\)
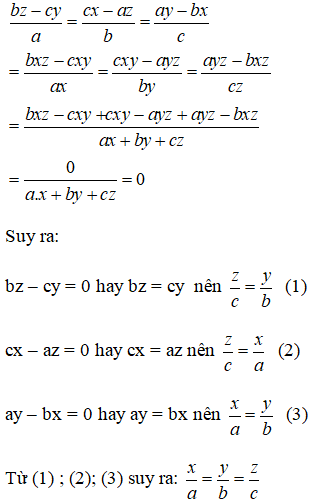
\(\dfrac{yc-bz}{x}=\dfrac{za-xc}{y}=\dfrac{xb-ya}{z}\)
\(\Rightarrow\dfrac{xyc-xbz}{x^2}=\dfrac{yza-xyc}{y^2}=\dfrac{xbz-yza}{z^2}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{xyc-xbz}{x^2}=\dfrac{yza-xyc}{y^2}=\dfrac{xbz-yza}{z^2}\)
\(=\dfrac{xyc-xbz+yza-xyc+xbz-yza}{x^2+y^2+z^2}=0\)
\(\Rightarrow\left\{{}\begin{matrix}yc=bz\\za=xc\\xb=ya\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{y}{b}=\dfrac{z}{c}\\\dfrac{x}{a}=\dfrac{z}{c}\\\dfrac{x}{a}=\dfrac{y}{b}\end{matrix}\right.\Leftrightarrow\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\left(đpcm\right)\)