Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AMDN có
\(\widehat{AMD}=\widehat{AND}=\widehat{MAN}=90^0\)
Do đó: AMDN là hình chữ nhật
b: AC=8cm
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{8\cdot6}{2}=24\left(cm^2\right)\)
c: Ta có: D và E đối xứng nhau qua AB
nên AD=AE
=>ΔADE cân tại A
mà AB là đường trung trực
nên AB là tia phân giác của góc DAE(1)
Ta có: D và F đối xứng nhau qua AC
nên AC là đường trung trực của DF
=>AD=AF
=>ΔADF cân tại A
mà AC là đường trung trực của DF
nên AC là tia phân giác của góc DAF(2)
Từ (1) và (2) suy ra \(\widehat{FAE}=2\cdot\left(\widehat{BAD}+\widehat{CAD}\right)=2\cdot90^0=180^0\)
Do đó: F,A,E thẳng hàng

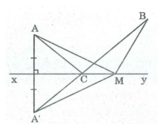
Vì A' đối xứng với A qua xy
⇒ xy là đường trung trực của AA'.
⇒ CA' = CA (t/chất đường trung trực)
MA' = MA (t/chất đường trung trực)
AC + CB = A'C + CB = A'B (1)
MA + MB = MA'+ MB (2)
Trong ∆ MA'B, ta có:
A'B < A'M + MB (bất đẳng thức tam giác) (3)
Từ (1), (2) và (3) suy ra: AC + CB < AM + MB
* Phân tích
Giả sử điểm M thuộc xy đã tìm được để có MA+ MB là ngắn nhất.
Lấy A’ đối xứng với A qua xy
ta có: MA = MA’
suy ra MA’ + MB cũng ngắn nhất .
Mà A và B lại nằm trên hai nửa mặt phẳng đối nhau có bờ là đường thẳng xy
Nên M phải nằm giữa A’và B tức là MA’ + MB = A’B
Suy ra M phải là giao của A’B và xy.
* Cách dựng
Dựng A’ đối xứng với A qua xy,
Nối A’với B cắt xy tại điểm M
*Chứng minh :
Nối M với A ta có MA = MA’ (A và A’ đối xứng với nhau qua xy)
Mà MA’ + MB = A’B
suy ra MA+MB =A’B là ngắn nhất
Thật vậy: nếu lấy một điểm M’ thuộc xy mà M’ khác M ,
nối M’ với A’ và M’ với B
ta có tam giác M’A’B.
Do đó M’A’ + M’B > A’B
mà M’A’ = M’A’(tính chất đối xứng).