3 căn 3/5 nhé

nếu cần trình bày thì bn kẻ hình ra

rồi có ob=oa=oc

ad đl pytago cho tam giác vuoong nnhes

vẽ hình xong lấy thước đo

Ta có BC ⊥ OA ⇒ BE = EC

E là trung điểm của OA ⇒ OE = AE và OA=OB= 3cm

OE=\(\dfrac{OA}{2}\) =\(\dfrac{3}{2}\) = 1.5 cm

ΔHBO vuông tại E :

BE=\(\sqrt{OB^2-OE^2}\)

=\(\sqrt{3^2-1.5^2}\) =\(\dfrac{3\sqrt{3}}{2}\) cm

⇒ BC= 2BE

= 2. \(\dfrac{3\sqrt{3}}{2}\) = \(3\sqrt{3}\) cm

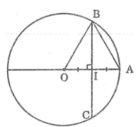
Gọi I là trung điểm của AB

Suy ra: IO = IA = (1/2).OA = 3/2

Ta có: BC ⊥ OA (gt)

Suy ra: góc (OIB) = 90 °

Áp dụng định lí Pitago vào tam giác vuông OBI ta có: O B 2 = B I 2 + I O 2

Suy ra:  B I 2 = O B 2 - I O 2

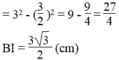
Ta có: BI = CI (đường kính dây cung)

- Gọi I là giao điểm của BC và OC

( IO = IA = 1,5cm ) ( OB = OA = 3cm )

Áp dụng đlí Py - ta - go cho tam giác vuông IBO ( ^I = 90^o ) , ta có :

\(OB^2=IB^2+IO^2\)

\(3^2=IB^2+1,5^2\)

\(IB^2=3^2-1,5^2=9-2,25=6,75\)

\(\Rightarrow IB=\sqrt{6,75}\approx2,6\)

Mà \(OA\perp BC\Rightarrow IC=IB\)( t/c đường kính vuông với dây cung )

=> BC = 2 . IB = 2 . 2,6 = 5,2

Vậy : BC = 5,2cm

Đáp án A

Gọi H là trung điểm của BC.

Do dây BC vuông góc với OA tại H nên ta có:

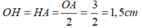
Áp dụng định lí Pytgo vào tam giác OHB vuông tại H ta có:

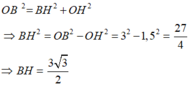
Theo định lí quan hệ vuông góc đường kính và dây ta có: H là trung điểm BC nên:

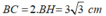
Ta có: OA = OB (bán kính)

    OB = BA (tính chất hình thoi).

Nên OA = OB = BA => ΔAOB đều => ∠AOB = 60o

Trong tam giác OBE vuông tại B ta có:

BE = OB.tg∠AOB = OB.tg60o = R.√3

a: Xét (O) có 

OI là một phần đường kính

BC là dây

OI\(\perp\)BC tại I

Do đó: I là trung điểm của BC

Xét tứ giác OBAC có

I là trung điểm của BC

I là trung điểm của OA

Do đó: OBAC là hình bình hành

mà OB=OC

nên OBAC là hình thoi

Xét ΔOAB có OA=OB=BA

nên ΔOAB đều

vì Dây BC của đường tròn vuông góc với OA tại trung điểm của OA, gọi giao điểm của BC với OA tại trung điểm OA là M

\(=>OM=AM=\dfrac{1}{2}OA=\dfrac{1}{2}.3=1,5cm\)

\(=>OB=OC=R=3cm\)=>tam giác OBC cân tại O có OM là đường cao nên cũng là trung tuyến=>OB=OC

pytago cho tam giác BMO

\(=>OB=OC=\sqrt{OB^2-OM^2}=\sqrt{3^2-1,5^2}=\dfrac{3\sqrt{3}}{2}cm\)

\(=>BC=OB+OC=3\sqrt{3}cm\)

a) Bán kính OA vuông góc với BC nên MB = MC.

Lại có MO = MA (gt).

Suy ra tứ giác OBAC là hình bình hành vì có các đường chéo cắt nhau tại trung điểm mỗi đường.

Lại có: OA ⊥ BC nên OBAC là hình thoi.

b) Ta có: OA = OB (bán kính)

    OB = BA (tính chất hình thoi).

Nên OA = OB = BA => ΔAOB đều  = >   ∠ A O B   =   60 °

Trong tam giác OBE vuông tại B ta có:

B E   =   O B . t g ∠ A O B   =   O B . t g 60 °   =   R . √ 3