Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

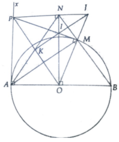
a, HS tự làm
b, Ta có OP ⊥ AM, BM ⊥ AM => BM//OP
c, chứng minh ∆AOP = ∆OBN => OP=BN
lại có BN//OP do đó OPNB là hình bình hành
d, Ta có ON ⊥ PI, PM ⊥ JO mà PM ∩ ON = I => I là trực tâm ∆POJ => JI ⊥ PO(1)
Chứng minh PAON hình chữ nhật => K trung điểm PO
Lại có A P O ^ = O P I ^ = I O P ^ => ∆IPO cân tại I => IKPO (2)
Từ (1),(2) => J,I,K thẳng hàng

a, PM là tiếp tuyến
=> PM vuông góc vớiOM
=>OMP=90
PA là tiếp tuyến
=>PA vuông AO
=>PAO=90
=>OMP+ PAO=180
=>Tứ giác APMO nội tiếp đường tròn
b, Góc AMB là góc nội tiếp hẳn nửa đường tròn
=> AMB=90=>AM vuông góc với MB
Lại có PA và PM là 2 tiếp tuyến cắt nhau tại M => PA=PM
=> P thuộc đường trung trực của AM
mà OA=OM
=> O thuộc đường trung trực của AM
=> PO là đường trung trực của AM => PO vuông góc với AM
=> PO // MB ( vì cùng vuông góc với AM)
a)\(\widehat{PAO}+\widehat{PMO}=180^o\)
=>APMO nội tiếp
b)Có:\(\widehat{BMO}=\widehat{MBO}=\widehat{MOP}\)(cùng \(=\frac{1}{2}sđ\stackrel\frown{AM}\))
\(\Rightarrow\text{}\text{}\text{}\text{}\widehat{BMO}=\widehat{MOP}\)(ở vị trí SLT)
=> BM//OP.
c)PN//OB(\(\perp AB\)); BM//OP (cmt)
=> BOPN là hình bình hành.
d)Có: AONP là hcn(\(\widehat{PAO}=\widehat{AON}=\widehat{ONP}=90^o\))
\(\Rightarrow PK=KO\)
mà OPMN nt(\(\widehat{PMO}=\widehat{PNO}\))
=> IM.IN=IP.IO
\(\Rightarrow\frac{IM}{IP}=\frac{IN}{IO}\)
mà \(NO=PA=PM\)
\(\Rightarrow\frac{IM}{IM+PM}=\frac{IN}{IN+PM}\)\(\Rightarrow IM=IN\)
\(\Rightarrow\Delta IPO\) cân tại I.
mà IK là trung tuyến ứng với PO
=> IK là đcao.
Có: OM và PN là đcao và OM\(\cap PN=\left\{J\right\}\)
\(\Rightarrow IJ\) là đcao ứng với PO
=> I,J,K thẳng hàng.
Đúng chưa Nguyễn Việt Lâm ?