
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



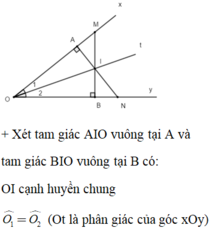
Do đó: Δ A I O = Δ B I O (cạnh huyền – góc nhọn)
Suy ra OA = OB ; IA = IB (hai cạnh tương ứng)
+ Xét tam giác IAM vuông tại A và tam giác IBN vuông tại B có:
IA = IB (cmt)


a: Xét ΔOIA vuông tại A và ΔOIB vuông tại B có
OI chung
\(\widehat{AOI}=\widehat{BOI}\)
Do đó: ΔOIA=ΔOIB
b: Xét ΔOAD vuông tại A và ΔOBC vuông tại B có
OA=OB
\(\widehat{BOC}\) chung
Do đó: ΔOAD=ΔOBC
Suy ra: OD=OC
Xét ΔOIC và ΔOID có
OC=OD
\(\widehat{COI}=\widehat{DOI}\)
OI chung
Do đó: ΔOIC=ΔOID
c: Ta có: ΔOCD cân tại O
mà OI là đường phân giác
nên OI là đường cao

a: Xét ΔOIA vuông tại A và ΔOIB vuông tại B có
OI chung
\(\widehat{AOI}=\widehat{BOI}\)
Do đó: ΔOIA=ΔOIB
b: Xét ΔOBC vuông tại B và ΔOAD vuông tại A có
OB=OA
\(\widehat{BOC}\) chung
Do đó: ΔOBC=ΔOAD
Suy ra: OC=OD
Xét ΔOIC và ΔOID có
OI chung
\(\widehat{COI}=\widehat{DOI}\)
OC=OD
Do đó: ΔOIC=ΔOID
c: Ta có: ΔOCD cân tại O
mà OI là đường phân giác
nên OI là đường cao

a) Xét \(\Delta OIH,\Delta OIK\) có :
\(\widehat{OHI}=\widehat{OKI}\left(=90^o\right)\)
\(OI:Chung\)
\(\widehat{IOH}=\widehat{IOK}\) (Ot là tia phân giác của \(\widehat{O}\); \(I\in Ot\))
=> \(\Delta OIH=\Delta OIK\) (cạnh huyền - góc nhọn)
=> IH= IK (2 cạnh tương ứng)
b) Xét \(\Delta IHM,\Delta IKN\) có :
\(\widehat{MHI}=\widehat{NKI}\left(=90^o\right)\)
\(IH=IK\left(cmt\right)\)
\(\widehat{MIH}=\widehat{NIK}\) (đối đỉnh)
=> \(\Delta IHM=\Delta IKN\) (cạnh huyền - góc nhọn)
=> \(IM=IN\) (2 cạnh tương ứng)
c) Xét \(\Delta OIH\perp H\) có :
\(IH^2=OI^2-OH^2\)(định lí PITAGO)
=> \(IH^2=10^2-8^2=36\)
=> \(IH=\sqrt{36}=6\left(cm\right)\)

1: Xét ΔOIC vuông tại I và ΔOID vuông tại I có
OI chung
\(\widehat{COI}=\widehat{DOI}\)
Do đó: ΔOIC=ΔOID
Suy ra: IC=ID
hay I là trung điểm của CD
2: Xét ΔOIA vuông tại A và ΔOIB vuông tại B có
OI chung
\(\widehat{AOI}=\widehat{BOI}\)
Do đó: ΔOIA=ΔOIB
Suy ra: IA=IB