a: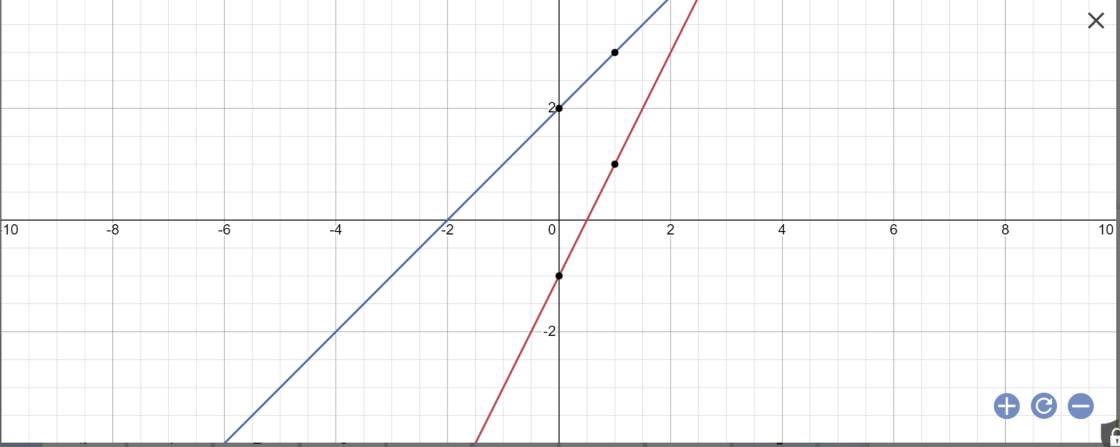 

b: Phương trình hoành độ giao điểm là:

2x-1=x+2

=>x=3

Thay x=3 vào y=x+2, ta được:

y=3+2=5

c: Vì (d)//(d1) nên (d): y=2x+b

Thay x=1 và y=0 vào (d), ta được:

b+2=0

=>b=-2

=>y=2x-2

b: Để hai đường thẳng cắt nhau tại một điểm trên trục tung thì m-1=15

hay m=16

Hoành độ giao điểm  \(d_1;d_2\)là nghiệm của phương trình \(2x-3=x-2\Rightarrow x=1\Rightarrow y=-1\Rightarrow A\left(1;-1\right)\)

Hoành độ giao điểm \(d_2;d_3\)là nghiệm của phương trình \(x-2=4x-2\Rightarrow x=0\Rightarrow y=-2\Rightarrow B\left(0;-2\right)\)

Hoành độ giao điểm \(d_1;d_3\)là nghiệm của phương trình \(2x-3=4x-2\Rightarrow x=-\frac{1}{2}\Rightarrow y=-4\Rightarrow C\left(-\frac{1}{2};-4\right)\)

Gọi \(G\left(\frac{x_A+x_B+x_C}{3};\frac{y_A+y_B+y_C}{3}\right)\)là trọng tâm tam giác ABC

Khi đó \(\frac{x_A+x_B+x_C}{3}=\frac{1+0-\frac{1}{2}}{3}=\frac{1}{6}\)

\(\frac{y_A+y_B+y_C}{3}=\frac{-1-2-4}{3}=-\frac{7}{3}\)

Vậy \(G\left(\frac{1}{6};-\frac{7}{3}\right)\) 

a) Vẽ tương đối (d1), (d2)    

b) Phương trình hoành độ giao điểm của (d1) và (d2):

\(\frac{3}{2}\)\(x+6\)\(=\) \(-3x-3\)

\(\Leftrightarrow\)\(\frac{9}{2}\)\(x=\)\(-9\)

\(\Leftrightarrow\)\(x=\)\(-2\)

\(\Rightarrow\)\(y=3\)

Vậy giao điểm của (d1) và (d2) là \(\left(-2;3\right)\)

c) Gọi phương trình đường thẳng cần tìm là (d): y = ax + b 

(d) // (d1) => (d):\(\frac{3}{2}\) \(x+b\)

A \(\in\)(d2) => A \((\)\(\frac{-4}{3}\)\(;1\)\()\)

Thay tọa độ A vào đường thẳng (d) ta có :

1 = \(\frac{3}{2}\) .\(\frac{-4}{3}\)+ b

\(\Leftrightarrow\)b = 3

Vậy (d): y =\(\frac{3}{2}\) \(x+3\)

:3

Tọa độ A là:

\(\left\{{}\begin{matrix}y=0\\\dfrac{3}{2}x-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=2\end{matrix}\right.\)

Tọa độ B là: 

\(\left\{{}\begin{matrix}y=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=3\end{matrix}\right.\)

Tọa độ C là:

\(\left\{{}\begin{matrix}\dfrac{3}{2}x-3=x-3\\y=x-3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{1}{2}x=0\\y=x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0-3=-3\end{matrix}\right.\)

Vậy: A(2;0); B(3;0); C(0;-3)

\(AB=\sqrt{\left(3-2\right)^2+\left(0-0\right)^2}=1\)

\(AC=\sqrt{\left(0-2\right)^2+\left(-3-0\right)^2}=\sqrt{13}\)

\(BC=\sqrt{\left(0-3\right)^2+\left(-3-0\right)^2}=3\sqrt{2}\)

Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)

\(=\dfrac{1+13-18}{2\cdot1\cdot\sqrt{13}}=\dfrac{-4}{2\sqrt{13}}=-\dfrac{2}{\sqrt{13}}\)

=>\(sinBAC=\sqrt{1-\left(-\dfrac{2}{\sqrt{13}}\right)^2}=\dfrac{3}{\sqrt{13}}\)

Diện tích tam giác ABC là:

\(S_{BAC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)

\(=\dfrac{1}{2}\cdot\dfrac{3}{\sqrt{13}}\cdot1\cdot\sqrt{13}=\dfrac{3}{2}\)