Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu A xảy ra tức là bắt được con thỏ trắng từ chuồng I. Vậy \(P\left( B \right) = \frac{7}{{10}}\)
Nếu A không xảy ra tức là bắt được con thỏ đen từ chuồng I. Vậy \(P\left( B \right) = \frac{7}{{10}}\)
Như vậy xác suất xảy ra của biến cố B không thay đổi bởi việc xảy ra hay không xảy ra của biến cố A.
Vì từ mỗi chuống bắt một con thỏ nên \(P\left( A \right) = \frac{{10}}{{15}} = \frac{2}{3}\) dù biến cố B xảy ra hay không xảy ra.
Vậy hai biến cố A và B độc lập.

a) \(P\left( A \right) = \frac{6}{{10}} = \frac{3}{5};P\left( B \right) = \frac{7}{8}\)
Không gian mẫu là tập hợp số cách Bạn Long lấy được một quả bóng từ hộp I và Bạn Hải lấy một quả bóng từ hộp II do đó \(n\left( \Omega \right) = 10.8 = 80\)
C: “Bạn Long lấy được quả màu trắng và bạn Hải lấy được quả màu đen”
Công đoạn 1: Bạn Long lấy được quả màu trắng có 6 cách
Công đoạn 2. Bạn Hải lấy được quả màu đen có 7 cách
Theo quy tắc nhân, tập hợp C có 6.7 = 42 (phần tử)
\(P\left( C \right) = P\left( {AB} \right) = \frac{{n\left( C \right)}}{{n\left( \Omega \right)}} = \frac{{42}}{{80}} = \frac{{21}}{{40}}\)
b) \(P\left( A \right).P\left( B \right) = \frac{3}{5}.\frac{7}{8} = \frac{{21}}{{40}}\)
Vậy P(AB) = P(A).P(B).

Không gian mẫu: \(C_{11}^2\)
a. Số cách lấy ra 2 viên cùng màu:
\(C_5^2+C_2^2+C_4^2\)
Số cách lấy ra 2 viên khác màu: \(C_{11}^2-\left(C_5^2+C_2^2+C_4^2\right)\)
Xác suất: \(P=\dfrac{C_{11}^2-\left(C_5^2+C_2^2+C_4^2\right)}{C_{11}^2}=...\)
b. Số cách lấy ra 2 viên không có bi đỏ nào: \(C_6^2\)
Số cách lấy ra ít nhất 1 bi đỏ: \(C_{11}^2-C_6^2\)
Xác suất: \(P=\dfrac{C_{11}^2-C_6^2}{C_{11}^2}=...\)

Không gian mẫu là kết quả của việc chọn ngẫu nhiên 4 con trong số 52 con
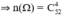
a. Đặt A : « Cả 4 con lấy ra đều là át »
⇒ n(A) = 1
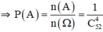
b. + B : « Không có con át nào trong 4 con khi lấy ra »
⇒ B là kết quả của việc chọn ngẫu nhiên 4 con trong số 48 con còn lại
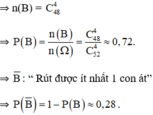
c. C: “Rút được 2 con át và 2 con K”.
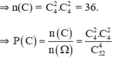

Chọn B
Số tập con của S là 2 6 = 64
Mỗi người có 64 cách chọn tập con, do vậy số phần tử của không gian mẫu là: 64 2
Ta tìm số cách chọn tập con thỏa mãn yêu cầu:
Giả sử tập con của A và B chọn được lần lượt có x,y phần tử ![]()
Khi đó: A có C 6 x cách chọn tập con, lúc này S còn 6 - x phần tử.
Ta chọn ra 2 phần tử gọi là a,b từ x phần tử trong tập con của A để xuất hiện trong tập con của B, có C x 2 cách.
Như vậy, tập con của B đã có 2 phần tử chung với tập con của A là a,b ta cần chọn thêm (y-2) phần tử khác trong (6-x) phần tử còn lại sau khi A đã chọn tập con,ở bước này có C 6 - x y - 2 cách chọn.
Vậy có: C 6 x C 6 - x y - 2 cách chọn tập con thỏa mãn.
Ta có điều kiện:
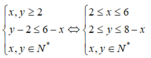
Cho x nhận các giá trị từ 2 đến 6, số cách chọn tập con thỏa mãn yêu cầu đề bài là:
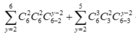
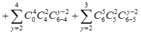
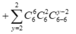
= 240 + 480 + 360 + 120 + 15 = 1215
Xác suất cần tính bằng: 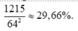

Phép thử T được xét là: "Từ cỗ bài tú lơ khơ 52 con bài, rút ngẫu nhiên 4 con bài".
Mỗi kết quả có thể có là một tổ hợp chập 4 của 52 con bài. Do đó số các kết quả có thể có của phép thử T là n(Ω) = C452 = = 270725.
Vì rút ngẫu nhiên nên các kết quả có thể có là đồng khả năng.
a) Gọi biến cố A: "Rút được bốn con át". Ta có, số kết quả có thể có thuận lợi cho A là n(A) = 1. Suy ra P(A) = ≈ 0,0000037.
b) Gọi biến cố B: "Rút được ít nhất một con át". Ta có
= "Rút được 4 con bài đều không là át". Mỗi kết quả có thể thuận lợi cho
là một tổ hợp chập 4 của 48 con bài không phải là át. Suy ra số các kết quả có thể có thuận lợi cho
là C448 =
= 194580. Suy ra P(
) =
≈ 0,7187.
Qua trên ta có P(B) = 1 - P() ≈ 0,2813.
c) Gọi C là biến cố: "Rút được hai con át và hai con K".
Mỗi kết quả có thể có thuận lợi cho C là một tổ hợp gồm 2 con át và 2 con K. Vận dụng quy tắc nhân tính được số các kết quả có thể có thuận lợi cho C là
n(C) = C24 C24 = 6 . 6 = 36.
Suy ra P(C) = ≈ 0,000133.

Có 2 hướng: tính xác suất bắt được 3 con trắng sau 5,6,7 lần bắt (3 trường hợp) hoặc tính xác suất bắt được 3 con trắng sau 3,4 lần bắt (2 trường hợp) rồi lấy 1 trừ đi kiểu phần bù.
- Bắt được 3 con trắng ngay sau 3 lần bắt đầu tiên: chọn 3 con bất kì từ 7 con có \(A_7^3\) cách chọn, chọn ra 3 con trắng từ 3 con trắng có \(A_3^3\) cách \(\Rightarrow P_1=\frac{A_3^3}{A_7^3}=\frac{1}{35}\)
- Bắt 3 con trắng sau 4 lượt, trong đó lượt 4 là con trắng, 3 lượt còn lại có 2 con trắng: chọn 4 con từ 7 con có \(A_7^4\) cách, chọn 1 con trắng từ 3 con trắng có \(P_3^1\) cách (lượt bắt cuối), chọn 2 con trắng và 1 con đen từ 6 con còn lại có \(C_2^2C_4^1.3!\Rightarrow P_2=\frac{P_3^1.C_3^2.C_4^1.3!}{A_7^4}=\frac{3}{35}\)
\(\Rightarrow P=1-\left(P_1+P_2\right)=\frac{31}{35}\)
Gọi \(A\) là biến cố: “Có 1 con cá mắt đen”, \(B\) là biến cố “Có 2 con cá mắt đen”.
Vậy \(A \cup B\) là biến cố “Có ít nhất 1 con cá mắt đen trong 2 con cá đó”.
Xác suất con cá là cá mắt đen là \(\frac{3}{4}\), xác suất con cá là cá mắt đỏ là \(\frac{1}{4}\)
\( \Rightarrow P\left( A \right) = \frac{3}{4}.\frac{1}{4} = \frac{3}{{16}};P\left( B \right) = \frac{3}{4}.\frac{3}{4} = \frac{9}{{16}}\)
Vì hai biến cố \(A\) và \(B\) xung khắc nên \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) = \frac{3}{{16}} + \frac{9}{{16}} = \frac{3}{4}\).