Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
.
.
.
.
Đáp án D
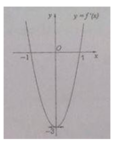
Phương trình hoành độ giao điểm của đồ thị f ( x ) và Ox: a x 4 + b x 2 + c = 0 .
Để phương trình có bốn nghiệm
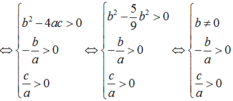
Gọi x 1 , x 2 , x 3 , x 4 lần lượt là bốn nghiệm của phương trình a x 4 + b x 2 + c = 0 và x 1 < x 2 < x 3 < x 4 . Không mất tính tổng quát, giả sử a > 0 .
Khi đó
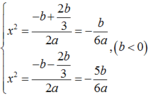
Suy ra x 1 = - - 5 b 6 a ; x 2 = - - b 6 a ; x 3 = - b 6 a ; x 4 = - b 6 a .
Do đồ thị hàm số f ( x ) nhận trục tung làm trục đối xứng nên ta có:
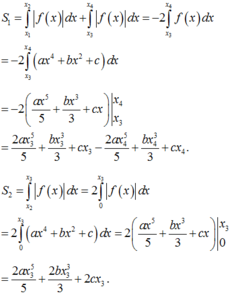
Suy ra
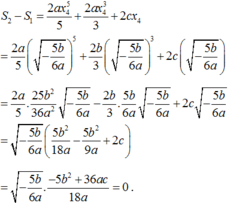
Vậy S 1 = S 2 hay S 1 S 2 = 1 .
.
Đáp án D
TXĐ: 
.
.
Yêu cầu bài toán suy ra đồ thị hàm số cắt trục 
tại 
điểm phân biệt nên:
+ 
có hai nghiệm phân biệt 
+ Tâm đối xứng 
của đồ thị hàm số phải thuộc trục 
.
Yêu cầu bài toán tương đương với 
.
Đáp án B
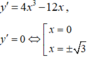
C m cắt trục hoành tại bốn điểm phân biệt khi
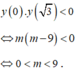
Gọi x 1 , x 2 , x 3 , x 4 lần lượt là hoành độ giao điểm của C m với trục hoành ( x 1 < x 2 < 0 < x 3 < x 4 ).
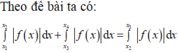
Do f(x) là hàm số chẵn và có hệ số a>0 nên
.
.
.
.
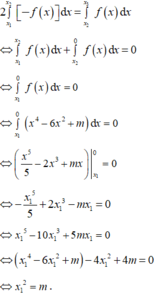
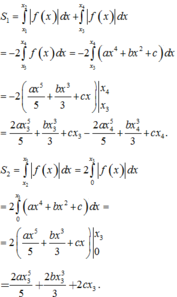
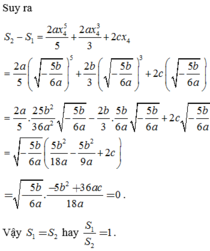
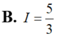
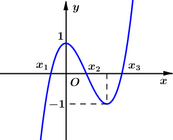
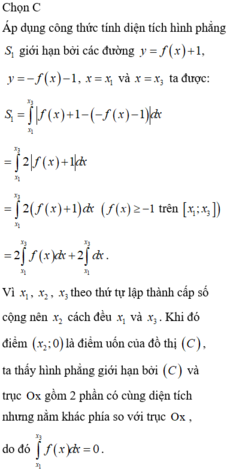
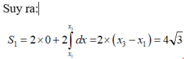
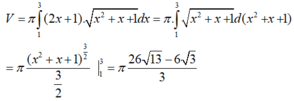
Đáp án B
Ta có: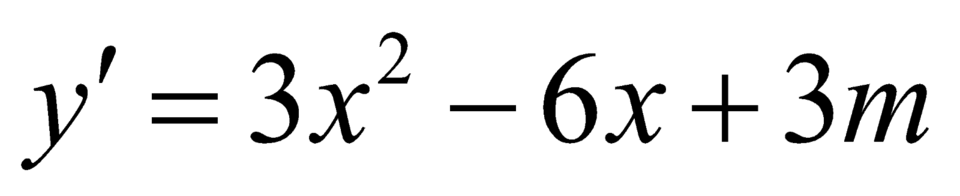
; 
.
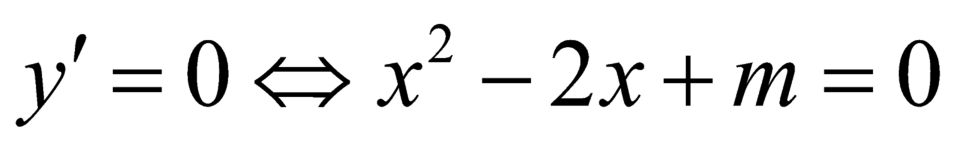hàm số có hai điểm cực trị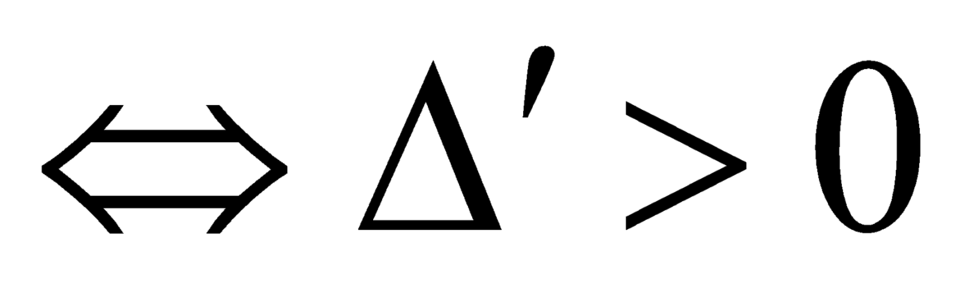
.
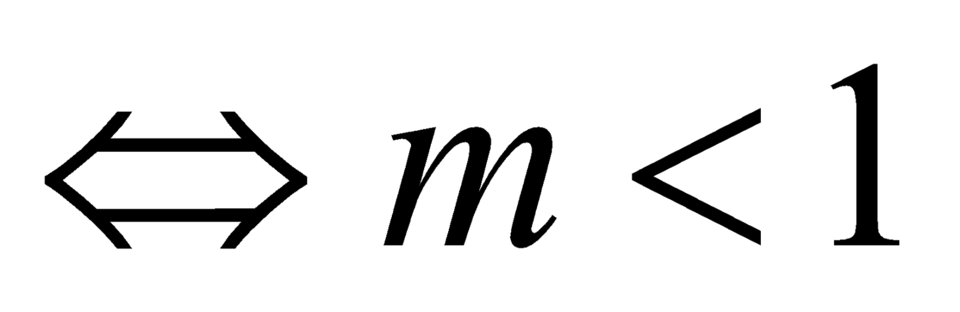Mặt khác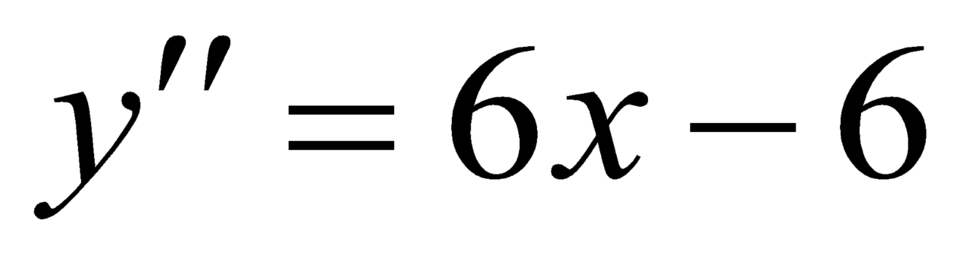
.
Hàm số bậc ba có đồ thị nhận điểm uốn làm tâm đối xứng. Do đó:
m cần tìm thoả và điểm uốn nằm trên trục hoành
=> m < 1 và