Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
Theo đề, ta có hệ:
\(\left\{{}\begin{matrix}-\dfrac{b}{2}=1\\0^2+b\cdot0+c=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2\\c=6\end{matrix}\right.\)
Bài 2:
Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-4}{2\cdot\left(-1\right)}=2\\y=-\dfrac{4^2-4\cdot\left(-1\right)\cdot0}{4\cdot\left(-1\right)}=\dfrac{16}{4}=4\end{matrix}\right.\)
=>Hàm số đồng biến khi x<2 và nghịch biến khi x>2

Đáp án :
B. Đồ thị hàm số chẵn nhận trục hoành làm trục đối xứng.

1) Hai đồ thị gọi là đối xứng với nhau qua trục hoành nếu f(x)+f(x)'=0
Do:
f(x)=x-2,f(x)'=2-x và f(x)+f(x)'=0=>Chúng đối xứng với nhau qua trục hoành.

a: Thay x=3 và y=0 vào (1), ta được:
\(6-3m=0\)
hay m=2

\(y=ax^2+bx+c\left(d\right)\)
Do y có gtln là 5 khi x=-2
\(\Rightarrow\left\{{}\begin{matrix}5=a\left(-2\right)^2+b\left(-2\right)+c\\-\dfrac{b}{2a}=-2\\a< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}4a-2b+c=5\\4a-b=0\end{matrix}\right.\)
Có \(M\in\left(d\right)\Rightarrow a+b+c=-1\)
Có hệ \(\left\{{}\begin{matrix}4a-2b+c=5\\4a+b=0\\a+b+c=-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{-2}{3}\\b=-\dfrac{8}{3}\\c=\dfrac{7}{3}\end{matrix}\right.\)(tm)
Vậy...

a: \(\left\{{}\begin{matrix}x_I=\dfrac{3}{2\cdot1}=\dfrac{3}{2}\\y_I=-\dfrac{\left(-3\right)^2-4\cdot1\cdot\left(-2\right)}{4\cdot1}=-\dfrac{17}{4}\end{matrix}\right.\)

Gọi công thức của hàm số bậc hai là \(y=ax^2+bx+c\)
Trục đối xứng là x=3 nên \(-\dfrac{b}{2a}=3\)
=>b=-2a
Thay x=0 và y=-16 vào (d), ta được:
\(a\cdot0^2+b\cdot0+c=-16\)
=>c=-16
=>\(y=ax^2+bx-16\)
Thay x=-2 và y=0 vào (d), ta được:
\(a\cdot\left(-2\right)^2+b\left(-2\right)-16=0\)
=>4a-2b-16=0
=>\(4a-2\cdot\left(-2a\right)=16\)
=>8a=16
=>a=2
=>b=-2a=-4
Vậy: Công thức cần tìm là \(y=2x^2-4x-16\)
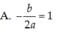
1: Theo đề, ta có:
-b/2*(-1)=5/2
=>-b/-2=5/2
=>b=5
2: y=-x^2+5x-4