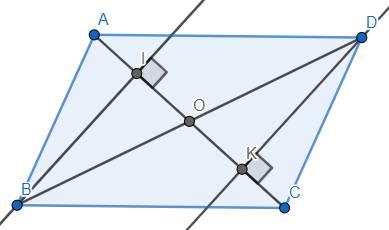
b) Vì BI vuông góc với AC tại I, nên I thuộc AC.

    Vì DK vuông góc với AC tại K, nên K thuộc AC.

    Vì O là giao điểm của AC và BD nên O thuộc AC.

    Suy ra I, O, K là các điểm thuộc AC; từ đó ba điểm I, O, K thẳng hàng

a. Do AB//CD nên góc ABD = BDC, ADB = CBD. Suy ra \(\Delta ABD=\Delta CDB\left(g-c-g\right)\Rightarrow AB=CD,AD=BC\)

b. Dễ thấy \(\Delta AOB=\Delta COD\left(g-c-g\right)\Rightarrow OA=OC,OB=OD\)

c. Xét tam giác ABC có AM và BO là các đường trung tuyến nên E là trọng tâm, vậy OB = 2EO.

Tương tự DF=2FO. Mà OD = OB. Vậy BE = EF = DF.

Xét tam giác ADM và tam giác CEM có:

ADM = CEM (= 90 độ)

AM = MC (M là trung điểm của AC)

AMD = CME (đối đỉnh)

=> tam giác ADM = tam giác CEM

=> DM = EM (2 cạnh tương ứng)

=> M là trung điểm của DE

b) ta có:

BD + BE = BD + BD + DE

mà ED = DM+EM và DM = EM

=> BD + BE = 2BD + 2DM = 2BM

trong tam giác ABM có A là góc vuông

=> AB^2 + AM^2 = BM^2 (định lí Pytago)

=> AB<BM

=> 2AB < 2BM

=> 2AB < BD+BE

a: AC=căn 10^2-5^2=5*căn 3(cm)

b: Xét ΔABD vuông tại A và ΔEBD vuông tại E có

BD chung

góc ABD=góc EBD

=>ΔBAD=ΔBED

c: Sửa đề: ΔBEF=ΔBAC

Xét ΔBEF vuông tại E và ΔBAC vuông tại A có

BE=BA

góc FBE chung

=>ΔBEF=ΔBAC