Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, sửa tìm các tam giác đồng dạng nhé
Xét tam giác AME và tam giác ADC ta có : ME // DC
\(\frac{AM}{MD}=\frac{AE}{CE}\)( theo định lí Ta lét )
^A chung
Vậy tam giác AME ~ tam giác ADC ( c.c.c )
\(\Rightarrow\frac{ME}{DC}=\frac{AE}{AC}\)( tỉ số đồng dạng )
b, Xét tam giác ADC ta có : ME // DC
\(\Rightarrow\frac{AM}{AD}=\frac{AE}{AC}=\frac{ME}{DC}\)( theo hệ quả Ta lét )
Xét tam giác ACB ta có : EN // AB
\(\Rightarrow\frac{CE}{AC}=\frac{CN}{BC}=\frac{EN}{AB}\)( theo hệ quả Ta lét )
giả sử : E là trung điểm MN khi \(\frac{ME}{DC}=\frac{NE}{AB}\)
mà \(DC=AB\)( do ABCD là hình bình hành )
Suy ra : \(ME=NE\)hay E là trung điểm MN

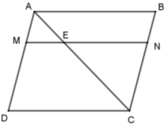
Vì ABCD là hình bình hành nên ME // DE và EN // AB.
+ ME // DC nên ΔAME ~ ΔADC, tỉ số đồng dạng A E A C = 1 3
+ Vì ABCD là hình bình hành nên góc B = D; AD = BC; AB = DC
=> ΔCBA ~ ΔADC
ΔCBA ~ ΔADC, tỉ số đồng dạng bằng 1
+ EN // AB nên ΔCNE ~ ΔADC, do đó ΔCNE ~ ΔADC, tỉ số đồng dạng C E A C = 2 3
Vậy cả (I), (II), (III) đều đúng.
Đáp án: C

Bài 6 :
Tự vẽ hình nhá :)
a) Gọi O là giao điểm của AC và EF
Xét tam giác ADC có :
EO // DC => AE/AD = AO/AC (1)
Xét tam giác ABC có :
OF // DC
=> CF/CB = CO/CA (2)
Từ (1) và (2) => AE/AD + CF/CB = AO/AC + CO/CA = AO + CO/AC = AC/AC = 1 => đpcm
Bài 7 :
a) Do EF // AB => CF / CA = EF / AB => CF / EF = AC / AB (1)
Dựng MG // AC và M là trung điểm của cạnh BC => GM là đường trung bình của tam giác ABC => G là trung điểm của cạnh AB =>AG = BG
Do DK // GM => AD / AG = DK / GM => AD / BG = DK / GM
=> DK / AD = GM / BG = \(\frac{\frac{AC}{2}}{\frac{AB}{2}}=\frac{AC}{AB} \left(2\right)\)
Từ (1) và (2) => CF / EF = DK / AD
Mà tứ giác ADEF là hình bình hành ( vì EF // AD và DE // AF ) nên AD = È
=> CF = DK ( đpcm )
Bài 8 :
Ta có : AB = AM + MB = 11 + 8 = 19 ( cm )
Áp dụng hệ quả định lí Ta-lét vào tam giác ABC, ta có :
AM / AB = AN / AC => AM + AB / AB = AN + AC / AC => 19 + 11 / 19 = AN + 38 / 38 => 30/19 = 38 + AN / 38
=> 1140 = 19.AN + 722
=> AN = ( 1140 - 722 ) / 19 = 22 ( cm )
=> NC = 38 - 12 = 26 ( cm )

a) Chứng minh được MN//PQ (cùng vuông góc với AC). Chứng minh được MP = QN. Þ ĐPCM.
b) Ta có:
S M N E = 1 2 S M E N C , S N P E = 1 2 S P B N E , S P Q E = 1 2 S , A P E Q S M Q E = 1 2 S Q E M D ⇒ S M N P Q = 1 2 S A B C S .
c) Chu vi MNPQ = MN + PQ + NP + QM
= EC + AE + BE + ED = AC + BE + ED.
Trong tam giác BED, BE + ED ³ BD
Þ Chu vi MNPQ ≥ AC + BD
Þ E là tâm của hình vuông ABCD

a) Học sinh tự chứng minh
b) nếu AEDF là hình thoi thì AD là phân giác của F A E ^ suy ra AD là phân giác của B A C ^
a: Xét ΔAME và ΔADC có
\(\widehat{AME}=\widehat{ADC}\)(hai góc đồng vị, ME//DC)
\(\widehat{MAE}\) chung
Do đó: ΔAME đồng dạng với ΔADC
=>\(\dfrac{AM}{AD}=\dfrac{ME}{DC}=\dfrac{AE}{AC}=\dfrac{1}{3}\)
Xét ΔCEN và ΔACD có
\(\widehat{CEN}=\widehat{ACD}\)(hai góc so le trong, EN//CD)
\(\widehat{ECN}=\widehat{CAD}\)(hai góc so le trong, CN//AD)
Do đó: ΔCEN đồng dạng với ΔACD
=>\(\dfrac{CE}{AC}=\dfrac{EN}{CD}=\dfrac{CN}{AD}=\dfrac{2}{3}\)
b: E là trung điểm của MN
=>EM=EN
Xét ΔEAM và ΔECN có
\(\widehat{EAM}=\widehat{ECN}\)(hai góc so le trong, AM//CN)
\(\widehat{AEM}=\widehat{CEN}\)(hai góc đối đỉnh)
Do đó: ΔEAM đồng dạng với ΔECN
=>\(\dfrac{EA}{EC}=\dfrac{EM}{EN}=1\)
=>E là trung điểm của AC