Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAME và ΔADC có
\(\widehat{AME}=\widehat{ADC}\)(hai góc đồng vị, ME//DC)
\(\widehat{MAE}\) chung
Do đó: ΔAME đồng dạng với ΔADC
=>\(\dfrac{AM}{AD}=\dfrac{ME}{DC}=\dfrac{AE}{AC}=\dfrac{1}{3}\)
Xét ΔCEN và ΔACD có
\(\widehat{CEN}=\widehat{ACD}\)(hai góc so le trong, EN//CD)
\(\widehat{ECN}=\widehat{CAD}\)(hai góc so le trong, CN//AD)
Do đó: ΔCEN đồng dạng với ΔACD
=>\(\dfrac{CE}{AC}=\dfrac{EN}{CD}=\dfrac{CN}{AD}=\dfrac{2}{3}\)
b: E là trung điểm của MN
=>EM=EN
Xét ΔEAM và ΔECN có
\(\widehat{EAM}=\widehat{ECN}\)(hai góc so le trong, AM//CN)
\(\widehat{AEM}=\widehat{CEN}\)(hai góc đối đỉnh)
Do đó: ΔEAM đồng dạng với ΔECN
=>\(\dfrac{EA}{EC}=\dfrac{EM}{EN}=1\)
=>E là trung điểm của AC

a, sửa tìm các tam giác đồng dạng nhé
Xét tam giác AME và tam giác ADC ta có : ME // DC
\(\frac{AM}{MD}=\frac{AE}{CE}\)( theo định lí Ta lét )
^A chung
Vậy tam giác AME ~ tam giác ADC ( c.c.c )
\(\Rightarrow\frac{ME}{DC}=\frac{AE}{AC}\)( tỉ số đồng dạng )
b, Xét tam giác ADC ta có : ME // DC
\(\Rightarrow\frac{AM}{AD}=\frac{AE}{AC}=\frac{ME}{DC}\)( theo hệ quả Ta lét )
Xét tam giác ACB ta có : EN // AB
\(\Rightarrow\frac{CE}{AC}=\frac{CN}{BC}=\frac{EN}{AB}\)( theo hệ quả Ta lét )
giả sử : E là trung điểm MN khi \(\frac{ME}{DC}=\frac{NE}{AB}\)
mà \(DC=AB\)( do ABCD là hình bình hành )
Suy ra : \(ME=NE\)hay E là trung điểm MN

Vì ΔDHE ~ ΔABC với tỉ số đồng dạng 2 3 nên tỉ số hai đường cao tương ứng của ΔDHE và ΔABC là 2 3 và tỉ số diện tích của ΔDHE và ΔABC là ( 2 3 ) 2 = 4 9
Do đó (I) và (IV) đúng, (II) và (III) sai.
Đáp án: A

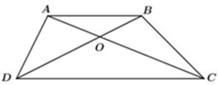
Vì AB // CD, áp dụng định lý Talet, ta có: O A O C = A B C D = O B O D
=> O A O C = A B C D ó OA.OD = OB.OC
=> Khẳng định (I) O A O C = A B C D đúng, khẳng định (II) O B O C = B C A D sai, khẳng định (III) OA.OD = OB.OC đúng
Vậy có 2 khẳng định đúng.
Đáp án: B
Vì ABCD là hình bình hành nên ME // DE và EN // AB.
+ ME // DC nên ΔAME ~ ΔADC, tỉ số đồng dạng A E A C = 1 3
+ Vì ABCD là hình bình hành nên góc B = D; AD = BC; AB = DC
=> ΔCBA ~ ΔADC
ΔCBA ~ ΔADC, tỉ số đồng dạng bằng 1
+ EN // AB nên ΔCNE ~ ΔADC, do đó ΔCNE ~ ΔADC, tỉ số đồng dạng C E A C = 2 3
Vậy cả (I), (II), (III) đều đúng.
Đáp án: C