Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Gọi số mặt của hình chóp là n
=> số mặt bên của hình chóp là n-1. Suy ra số cạnh của đa giác đáy hình chóp có n-1 cạnh.
Vậy số cạnh bên của hình chóp là 20-(n-1)=21-n
Mặt khác số cạnh bên của hình chóp bằng số mặt bên của hình chóp nên ta có
=> n-1=21-n=> n=11

Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
Gọi M là trung điểm AB \(\Rightarrow AB\perp OM\Rightarrow AB\perp\left(SOM\right)\)
\(\Rightarrow\widehat{SMO}\) là góc giữa mặt bên và đáy hay \(\widehat{SMO}=60^0\)
\(SO=OM.tan\widehat{SMO}=\dfrac{a}{2}.tan60^0=\dfrac{a\sqrt{3}}{2}\)
\(V=\dfrac{1}{3}SO.S_{ABCD}=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{2}.a^2=\dfrac{a^3\sqrt{3}}{6}\)

Gọi \(I\) là tâm của đáy \(ABCD\) (giao điểm của \(AC\) và \(BD\))
a) Vì đây là hính chóp đều nên có ngay \(SI\) là đường cao kẻ từ S
\(SI=\sqrt{SA^2-AI^2}=\sqrt{SA^2-\frac{AB^2}{2}}=a\sqrt{2}\)
\(V_{S.ABCD}=\frac{1}{3}.SI.S_{ABCD}=\frac{4a^3\sqrt{2}}{3}\)
b) Thấy ngay \(IA=IB=IC=ID=IS=a\sqrt{2}\)
suy ra tâm mc ngoại tiếp là \(I\) và \(R=a\sqrt{2}\)
c) bạn dùng công thức sau để tính bán kính mặt cầu nội tiếp
\(r=\frac{3V_{S.ABCD}}{S_{ABCD}+4S_{SAB}}=\frac{\frac{4a^3\sqrt{2}}{3}}{4a^2+4.\frac{a^2\sqrt{3}}{2}}=\frac{4\sqrt{2}-2\sqrt{6}}{3}.a\)
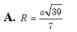
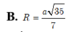
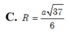
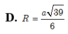


Chọn B
Số cạnh bên của hình chóp bằng số cạnh đáy.
Suy ra số cạnh bên của hình chóp là: 20 2 = 10 cạnh.
Vậy hình chóp có 10 mặt bên và 1 mặt đáy.