Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) () // (ABCD) =>
// AB =>
là trung điểm của SB. Chứng minh tương tự với các điểm còn lại
b) Áp dụng định lí Ta-lét trong không gian:
\(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}\).
Do \(A_1A_2=A_2A\) nên : \(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}=1\).
Nên \(B_1B_2=B_2B;C_1C_2=CC_2=D_1D_2=D_2D\).
c) Có hai hình chóp cụt:

Ta có:
\({a_1} = 0;{a_2} = 1;{a_3} = 2;{a_4} = 3;{a_5} = 4\).
\({b_1} = 2.1 = 2;{b_2} = 2.2 = 4;{b_3} = 2.3 = 6;{b_4} = 2.4 = 8\).
\({c_1} = 1;{c_2} = {c_1} + 1 = 1 + 1 = 2;{c_3} = {c_2} + 1 = 2 + 1 = 3;{c_4} = {c_3} + 1 = 3 + 1 = 4\).
+ Chu vi đường tròn có bán kính \(n\) là \({d_n} = 2\pi n\).
Ta có: \({d_1} = 2\pi .1 = 2\pi ;{d_2} = 2\pi .2 = 4\pi ;{d_3} = 2\pi .3 = 6\pi ;{d_4} = 2\pi .4 = 8\pi \).

Số vecto tạo từ 2n điểm là: \(A_{2n}^2\)
Đa giác đều 2n đỉnh có n đường chéo, cứ 2 đường chéo cho ta 1 hình chữ nhật tương ứng, do đó số hình chữ nhật có đỉnh là đỉnh của đa giác đều là: \(C_n^2\)
\(\Rightarrow A_{2n}^2=9C_n^2\Leftrightarrow\dfrac{\left(2n\right)!}{\left(2n-2\right)!}=\dfrac{9.n!}{2!.\left(n-2\right)!}\)
\(\Leftrightarrow2n\left(2n-1\right)=\dfrac{9n\left(n-1\right)}{2}\)
\(\Leftrightarrow n=5\)
dạ em chưa hiểu tại sao số vecto tạo từ 2n điểm và số hình chữ nhật có đỉnh là đỉnh của đa giác đều lại ra được như kia vậy ạ :(((

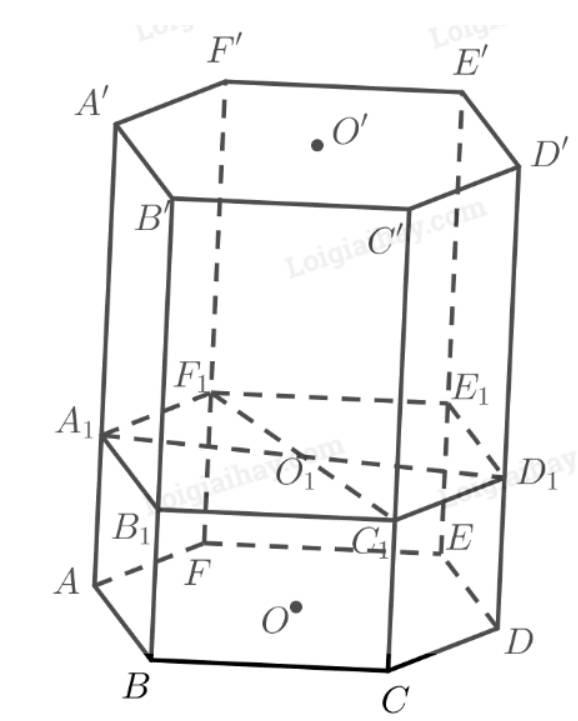
a) Gọi \({B_1},{E_1}\) lần lượt là giao điểm của \(mp\left( {{A_1}{D_1},{F_1}{C_1}} \right)\) với \(BB',EE'\).
Ta có:
\(\left. \begin{array}{l}{A_1}{D_1}\parallel \left( {ABC{\rm{DEF}}} \right)\\{F_1}{C_1}\parallel \left( {ABC{\rm{DEF}}} \right)\\{A_1}{D_1},{F_1}{C_1} \subset mp\left( {{A_1}{D_1},{F_1}{C_1}} \right)\end{array} \right\} \Rightarrow mp\left( {{A_1}{D_1},{F_1}{C_1}} \right)\parallel \left( {ABC{\rm{DEF}}} \right)\)
Vậy giao tuyến của \(mp\left( {{A_1}{D_1},{F_1}{C_1}} \right)\) với các mặt bên của lăng trụ là:
\(\begin{array}{l}mp\left( {{A_1}{D_1},{F_1}{C_1}} \right) \cap \left( {ABB'A'} \right) = {A_1}{B_1}\\mp\left( {{A_1}{D_1},{F_1}{C_1}} \right) \cap \left( {BCC'B'} \right) = {B_1}{C_1}\\mp\left( {{A_1}{D_1},{F_1}{C_1}} \right) \cap \left( {C{\rm{DD'C'}}} \right) = {C_1}{D_1}\\mp\left( {{A_1}{D_1},{F_1}{C_1}} \right) \cap \left( {DEE'D'} \right) = {D_1}{E_1}\\mp\left( {{A_1}{D_1},{F_1}{C_1}} \right) \cap \left( {EFF'E'} \right) = {E_1}{F_1}\\mp\left( {{A_1}{D_1},{F_1}{C_1}} \right) \cap \left( {AFF'A'} \right) = {A_1}{F_1}\end{array}\)
b) \(ABCDEF.A'B'C'D'E'F'\) là hình lăng trụ \( \Rightarrow CC' = AA' = 70\left( {cm} \right)\)
\(A'{A_1} = 6A{A_1} \Rightarrow A{A_1} = \frac{1}{7}AA' = 10\left( {cm} \right)\)
\(mp\left( {{A_1}{D_1},{F_1}{C_1}} \right)\parallel \left( {ABC{\rm{DEF}}} \right)\parallel \left( {A'B'C'{\rm{D'E'F'}}} \right)\)
\(\begin{array}{l} \Rightarrow \frac{{C{C_1}}}{{CC'}} = \frac{{A{A_1}}}{{AA'}} \Leftrightarrow C{C_1} = \frac{{CC'.A{A_1}}}{{AA'}} = \frac{{70.10}}{{70}} = 10\left( {cm} \right)\\ \Rightarrow {C_1}C' = CC' - C{C_1} = 70 - 10 = 60\left( {cm} \right)\end{array}\)



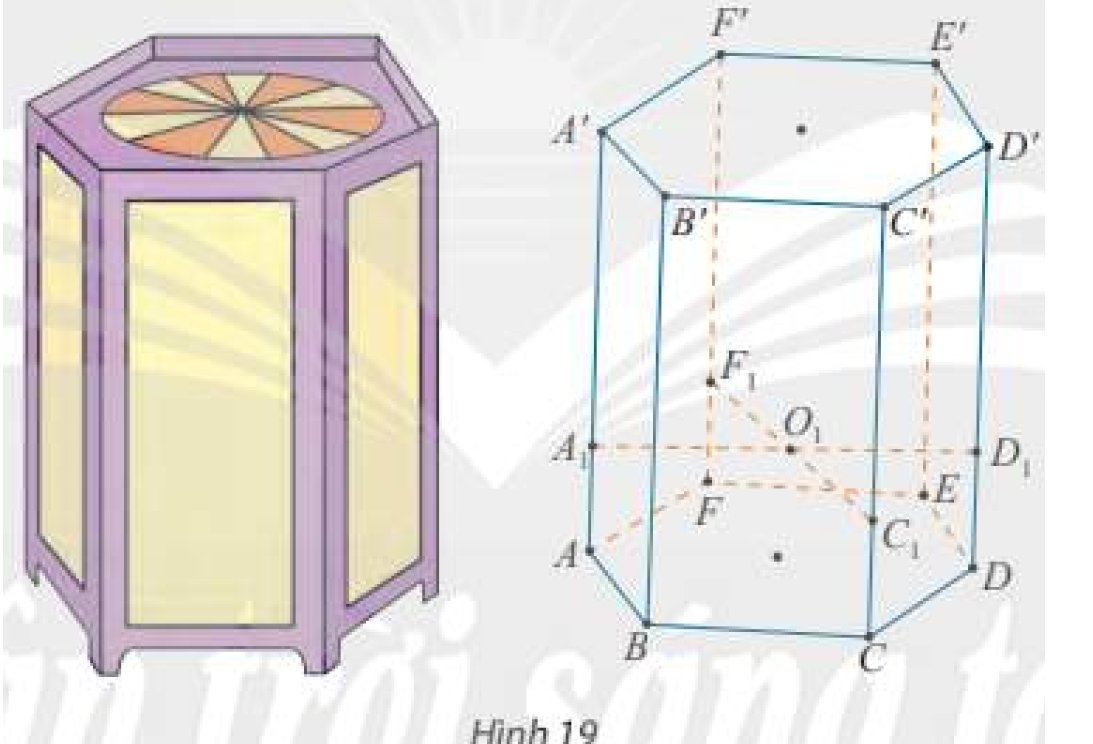
a) Ta có:
\(\begin{array}{l}\left( P \right)\parallel \left( {{A_1}{A_2}{A_3}...{A_6}} \right)\\ \Rightarrow {A_1}^\prime {A_2}^\prime \parallel {A_1}{A_2},{A_2}^\prime {A_3}^\prime \parallel {A_2}{A_3},{A_3}^\prime {A_4}^\prime \parallel {A_3}{A_4},{A_4}^\prime {A_5}^\prime \parallel {A_4}{A_5},{A_5}^\prime {A_6}^\prime \parallel {A_5}{A_6},{A_6}^\prime {A_1}^\prime \parallel {A_6}{A_1}\\ \Rightarrow \frac{{{A_1}^\prime {A_2}^\prime }}{{{A_1}{A_2}}} = \frac{{{A_2}^\prime {A_3}^\prime }}{{{A_2}{A_3}}} = \frac{{{A_3}^\prime {A_4}^\prime }}{{{A_3}{A_4}}} = \frac{{{A_4}^\prime {A_5}^\prime }}{{{A_4}{A_5}}} = \frac{{{A_5}^\prime {A_6}^\prime }}{{{A_5}{A_6}}} = \frac{{{A_6}^\prime {A_1}^\prime }}{{{A_6}{A_1}}}\end{array}\)
Mà \({A_1}{A_2} = {A_2}{A_3} = {A_3}{A_4} = {A_4}{A_5} = {A_5}{A_6} = {A_6}{A_1}\)
\( \Rightarrow {A_1}^\prime {A_2}^\prime = {A_2}^\prime {A_3}^\prime = {A_3}^\prime {A_4}^\prime = {A_4}^\prime {A_5}^\prime = {A_5}^\prime {A_6}^\prime = {A_6}^\prime {A_1}^\prime \)
Vậy đa giác \({A_1}^\prime {A_2}^\prime {A_3}^\prime ...{A_6}^\prime \) là lục giác đều.
b) Ta có:
\(\left. \begin{array}{l}O' \in {A_1}^\prime {A_4}^\prime \subset \left( {S{A_1}{A_4}} \right)\\O' \in {A_3}^\prime {A_6}^\prime \subset \left( {S{A_3}{A_6}} \right)\\\left( {S{A_1}{A_4}} \right) \cap \left( {S{A_3}{A_6}} \right) = SO\end{array} \right\} \Rightarrow O' \in SO\)
Mà \(S.{A_1}{A_2}{A_3}...{A_6}\) là hình chóp đều \( \Rightarrow SO \bot \left( {{A_1}{A_2}{A_3}...{A_6}} \right)\)
Vậy \(OO' \bot \left( {{A_1}{A_2}{A_3}...{A_6}} \right)\)