a, Ta có: \(\left\{{}\begin{matrix}AB\perp SA\left(do:SA\perp\left(ABCD\right)\right)\\AB\perp AD\left(gt\right)\end{matrix}\right.\)

\(\Rightarrow AB\perp\left(SAD\right)\)

Từ C kẻ CH // AB  ⇒ CH ⊥ (SAD)

⇒ d (C, (SAD)) = CH = 2a

b, Ta có: \(\left(SAC\right)\cap\left(ABCD\right)=AC\)

Hạ DE ⊥ AC ⇒ DE ⊥ (SAC)

⇒ d(D, (SAC)) = DE

Ta có: AC = 2a√2, AH = HC 2a và HD = a

Xét tam giác HDC vuông tại H, có: \(DC=\sqrt{HD^2+HC^2}=a\sqrt{5}\)

Xét tam giác AHC vuông cân tại H, có: \(\widehat{HAC}=45^o=\widehat{DAE}\)

Xét tam giác ADE vuông tại E, có: \(DE=AD.sin\widehat{DAE}=\dfrac{3a\sqrt{2}}{2}\)

a: SO vuông góc (ABCD)

=>(SAC) vuông góc (ABCD)

b: AC vuông góc BD

BD vuông góc SO

=>BD vuông góc (SAC)

=>(SBD) vuông goc (SAC)

a: SO vuông góc (ABCD)

=>(SAC) vuông góc (ABCD)

SO vuông góc (ABCD)

=>(SBD) vuông góc (ABCD)

b: BD vuông góc AC

BD vuông góc SA

=>BD vuông góc (SAC)

d: (SB;(ABCD))=(BS;BO)=góc SBO

cos SBO=OB/SB=a*căn 2/2/(a*căn 2)=1/2

=>góc SBO=60 độ

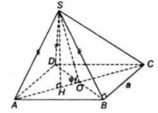
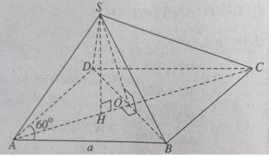
a) Tam giác ABD có AB = AD ( do ABCD là hình thoi)

=> Tam giác ABD cân tại A. Lại có góc A= 60o

=> Tam giác ABD đều.

Lại có; SA = SB = SD nên hình chóp S.ABD là hình chóp đều.

* Gọi H là tâm của tam giác ABD

=>SH ⊥ (ABD)

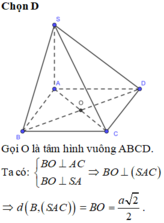
*Gọi O là giao điểm của AC và BD.

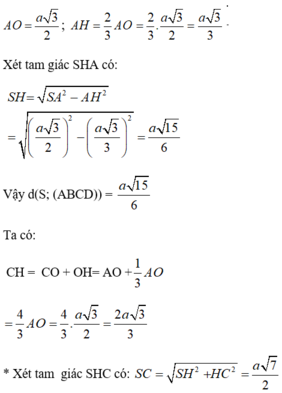
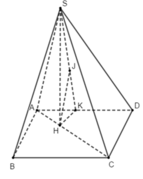
+ Kẻ SH ⊥ AC, H ∈  AC

Do (SAC)  ⊥ (ABCD) ⇒ SH  ⊥ (ABCD)

+ BD = 2a ⇒ AC = 2a

SA = A C 2 − S C 2 = 2 a 2 − a 3 2 = a ; SH =  S A . S C A C = a . a 3 2 a = a 3 2

Ta có: AH = S A 2 − S H 2 = a 2 − a 3 2 2 = a 2 ⇒ AC = 4AH

Lại có: HC ∩ (SAD) = A d C ; S A D d H ; S A D = A C A H =  4

⇒ d(C; (SAD)) = 4d(H; (SAD))

Do BC // (SAD) (BC//AD)  ⇒  d(B; (SAD)) = d(C; (SAD))

Do đó d(B; (SAD)) = 4d(H; (SAD))

+ Kẻ HK ⊥ AD tại K, kẻ HJ ⊥  SK tại J

Ta chứng minh được HJ ⊥  (SAD)  ⇒ d(H; (SAD)) = HJ

⇒  d(B; (SAD)) = 4HJ

+ Tính HJ

Tam giác AHK vuông tại K có H A K ^ = C A D ^ = 45 ° ⇒  HK = AH.sin 45 ° =  a 2 4

Mặt khác: 1 H J 2 = 1 H K 2 + 1 S H 2 ⇒ HJ =  a 21 14

Vậy d(B; (SAD)) = 4 . a 21 14 = 2 a 21 7 .

Đáp án C

Kẻ \(BK\perp AC\Rightarrow BK\perp\left(SAC\right)\)

\(\Rightarrow BK=d\left(B;\left(SAC\right)\right)\)

\(\dfrac{1}{BK^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Rightarrow BK=\dfrac{AB.AC}{\sqrt{AB^2+AC^2}}=\dfrac{a\sqrt{3}}{2}\)

Kẻ \(CP\perp BH\Rightarrow CP\perp\left(SBH\right)\)

\(\Rightarrow CP=d\left(C;\left(SBH\right)\right)\)

\(\widehat{CBP}=\widehat{ACB}=30^0\Rightarrow CH=BC.sin30^0=\dfrac{a\sqrt{3}}{2}\)

\(BH=\dfrac{AC}{2}=\dfrac{1}{2}\sqrt{AB^2+AC^2}=a\)\(\Rightarrow SH=\sqrt{SB^2-BH^2}=a\)

Kẻ \(HE\perp BC\) , kẻ \(HF\perp SE\Rightarrow HF=d\left(H;\left(SBC\right)\right)\)

\(HE=CH.sin30^0=\dfrac{a}{2}\) 

\(\dfrac{1}{HF^2}=\dfrac{1}{SH^2}+\dfrac{1}{HE^2}\Rightarrow HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{5}}{5}\)

a) Nhận xét: Tam giác ABD là tam giác đều. Gọi H là hình chiếu vuông góc của S xuống mặt phẳng (ABD), ta có:

Hình 3.91

SA = SB = SD ⇒ H là tâm đường tròn ngoại tiếp tam giác ABD

⇒ H là trọng tâm tam giác ABD

⇒ H ∈ AC.

⇒ (SAC) ⊥ (ABCD).

b) Ta có:

a: BD vuông góc AC

BD vuông góc SA

=>BD vuông góc (SAC)

=>(SBD) vuông góc (SAC)

b: BC vuông góc AB

BC vuông góc SA
=>BC vuông góc (SAB)

=>BC vuông góc AK

mà AK vuông góc SB

nên AK vuông góc (SBC)

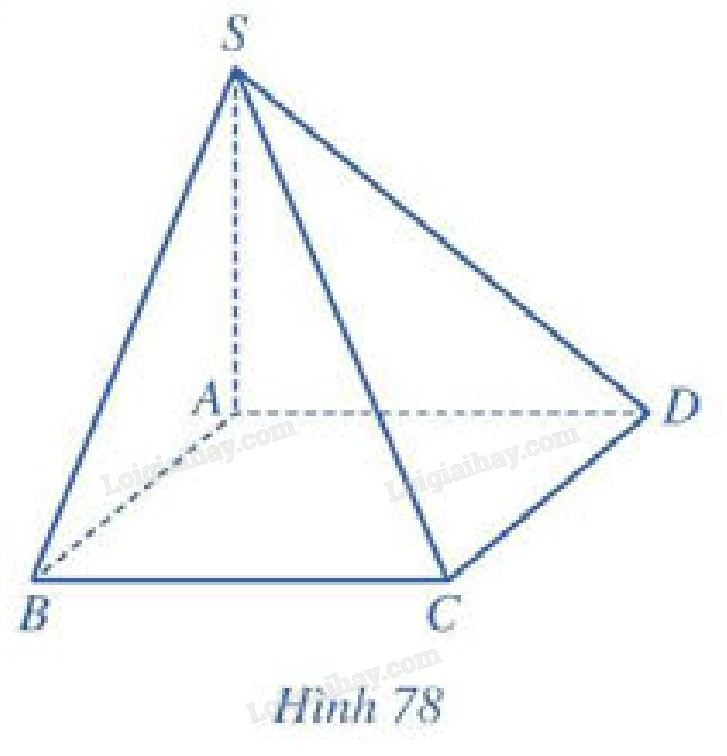
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot C{\rm{D}}\)

\(ABCD\) là hình vuông \( \Rightarrow A{\rm{D}} \bot C{\rm{D}}\)

\(\begin{array}{l} \Rightarrow C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot S{\rm{D}}\\ \Rightarrow d\left( {S,C{\rm{D}}} \right) = S{\rm{D}} = \sqrt {S{A^2} + A{{\rm{D}}^2}}  = a\sqrt 2 \end{array}\)

b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot A{\rm{D}}\)

\(ABCD\) là hình vuông \( \Rightarrow A{\rm{B}} \bot A{\rm{D}}\)

\( \Rightarrow A{\rm{D}} \bot \left( {SA{\rm{B}}} \right) \Rightarrow d\left( {D,\left( {SAB} \right)} \right) = A{\rm{D}} = a\)

c) Kẻ \(AH \bot S{\rm{D}}\left( {H \in S{\rm{D}}} \right)\).

\(C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot AH\)

\( \Rightarrow AH \bot \left( {SC{\rm{D}}} \right) \Rightarrow d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = AH\)

Tam giác \(SAD\) vuông tại \(A\) có đường cao \(AH\)

\( \Rightarrow AH = \frac{{SA.A{\rm{D}}}}{{S{\rm{D}}}} = \frac{{a\sqrt 2 }}{2}\)

Vậy \(d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = \frac{{a\sqrt 2 }}{2}\).