Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
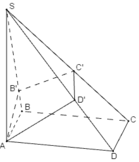
Dễ thấy BD ⊥ SC, nên BD // (AB'C'D'), suy ra BD // B'D'.
Gọi I = AC ∩ BD, J = AC' ∩ SI, khi đó J là trọng tâm của tam giác SAC và J ∈ B'D'.
Suy ra
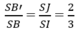
Do đó dễ thấy
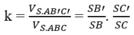

Phương pháp
+ Xác định góc giữa đường thẳng d và mặt phẳng (P) là góc giữa đường thẳng d và đường thẳng d' với d' là hình chiếu của d trên mặt phẳng (P).
+ Thể tích hình chóp có chiều cao h và diện tích đáy S là V = 1 3 h S
Cách giải:
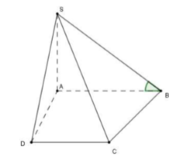
+ Ta có SA ⊥ (ABCD) => AB là hình chiếu của
SB lên mặt phẳng (ABCD) . Suy ra góc giữa SB và đáy là góc ∠ SBA = 600.
+ Xét tam giác vuông SAB có: ![]()
+ Diện tích đáy
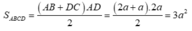
+ Thể tích khối chóp là
![]()
Chọn C.



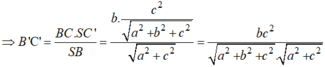
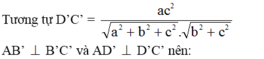 S
∆
A
B
'
C
'
=
1
2
B
'
C
'
.
A
B
'
=
1
2
.
c
2
a
2
+
c
2
.
b
a
2
+
b
2
+
c
2
.
c
a
a
2
+
c
2
S
∆
A
B
'
C
'
=
1
2
B
'
C
'
.
A
B
'
=
1
2
.
c
2
a
2
+
c
2
.
b
a
2
+
b
2
+
c
2
.
c
a
a
2
+
c
2
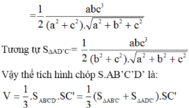
![]()
![]()
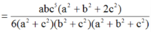

Chọn D
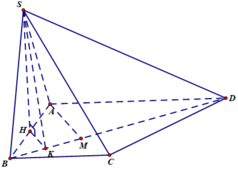
Ta có ![]()
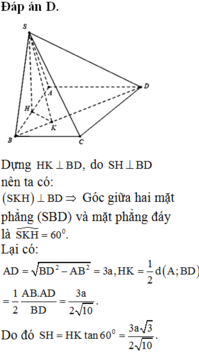
Gọi H là trung điểm AB thì ![]() ,
,
kẻ ![]() , ta có
, ta có ![]() là góc giữa (SBD) và (ABCD), do đó
là góc giữa (SBD) và (ABCD), do đó ![]() = 600
= 600
Gọi AM là đường cao của tam giác vuông ABD. Khi đó, ta có:
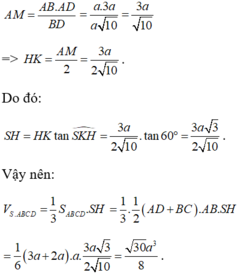

Chọn A.
Gọi H là trung điểm của CD, M là trung điểm của BC. Khi đó HM ⊥ BC, SM ⊥ BC. Dễ thấy tam giác HBC vuông cân ở H, do đó tính được BC, SM. Từ đó tính được SH.

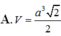
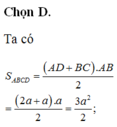
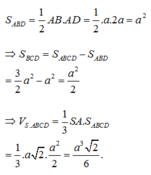
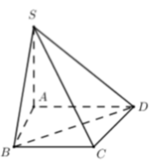
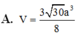
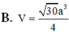
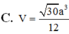
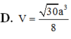
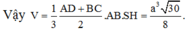

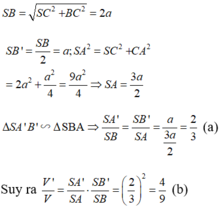
Chọn A