Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
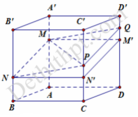
Lấy M’, N’ lần lượt trên các cạnh DD’ và CC’ sao cho M A = M ' D và N B = N ' C .
Vì A B B ' A ' / / C DD ' C ' nên 2 giao tuyến giữa mặt phẳng (MNP) lần lượt với các mặt phẳng (ABB'A') và (CDC'C') sẽ song song với nhau. Do vậy ta sẽ lấy Q ∈ DD ' sao cho M N / / P Q . Ta có:
D Q ' = D ' M ' − Q M ' = DD ' 3 − P C − N ' C = DD ' 3 − DD ' 2 − DD ' 3 = DD ' 6 ⇒ D ' Q DD ' = 1 6 .

Giả sử C(c,3-c). Gọi I là giao điểm của AC và MN, suy ra \(\overrightarrow{AI}=\dfrac{2}{3}\overrightarrow{AC}=\left(\dfrac{2(c+2)}{3};\dfrac{2(3-c)}{3}\right)\)
Do đó \(I\left(\dfrac{2c-2}{3};\dfrac{6-2c}{3}\right)\in MN:7x-6y-5=0\Rightarrow c=\dfrac{5}{2}\). Vậy \(C\left(\dfrac{5}{2};\dfrac{1}{2}\right)\)
Trung điểm của AC là \(P\left(\dfrac{1}{4};\dfrac{1}{4}\right),\overrightarrow{AC}\left(\dfrac{7}{2};\dfrac{1}{2}\right)\Rightarrow B\left(\dfrac{1}{4}+t;\dfrac{1}{4}-7t\right), D\left(\dfrac{1}{4}-t;\dfrac{1}{4}+7t\right)\).
Vì \(BP=CP=\dfrac{AC}{2}=\dfrac{5\sqrt{2}}{2}\)nên \(t=\pm\dfrac{1}{2}\)
Vậy \(B\left(\dfrac{3}{4};-\dfrac{13}{4}\right),D\left(-\dfrac{1}{4};\dfrac{15}{4}\right)\)hoặc \(B\left(-\dfrac{1}{4};\dfrac{15}{4}\right),D\left(\dfrac{3}{4};-\dfrac{13}{4}\right)\).

bài 1
\(A+B=a+b-5-b-c+1=a-c-4\)
\(A+B+C+D=a-c-4+b-c-4+b-a=2b-2c\)
\(A-B+C-D=a+b-5+b+c-1+b-c-4+a-b\)
\(A-B+C-D=2a+2b-10\)
\(A+B=a-c-4\)
\(C-D=b-c-4-b+a=a-c-4\)
\(A+B=C-D\)

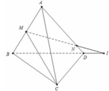


Đáp án A
Ta chứng minh được công thức tỷ số thể tích tối với khối hộp như sau (học sinh có thể tự chứng minh).
V A ' B ' C ' D ' . M N P Q V A " B ' C ' D ' . A B C D = 1 2 A ' M A ' A + C ' P C ' C = 1 2 B ' N B ' B + D Q D ' D
Khi đó: 1 3 + 1 2 = 2 3 + D Q D ' D ⇔ D Q D ' D = 1 6 .