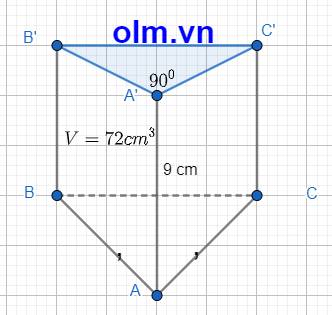
V_ABCA'B'C'  = S_ABC.h

Diện tích của tam giác ABC là: 72 : 9 = 8 (cm²)

S_ABC = \(\dfrac{1}{2}\)AB.AC = \(\dfrac{1}{2}\)AB² = 8 ⇒ AB² = 8.2 = 16 

⇒ AB = AC = \(\sqrt{16}\) = 4 (cm)

Vậy độ dài cạnh đáy AB dài 4cm

Diện tích đáy ABC của hình lăng trụ đứng là:

\(25:5=5\left(cm^2\right)\)

Độ dài của BC là:

\(S_{ABC}=\dfrac{1}{2}.AB.BC\)

\(\Rightarrow BC=\dfrac{2.S_{ABC}}{AB}=\dfrac{2.5}{2}=5\left(cm\right)\)

Vậy \(BC=5\left(cm\right)\)

Hình lăng trụ đứng tạo lập được là:

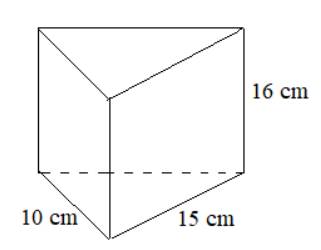
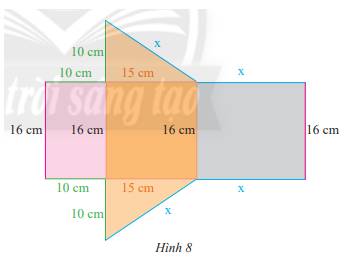
Độ dài 2 cạnh góc vuông của đáy là: 10 cm và 15 cm

Chiều cao của lăng trụ là: 16 cm

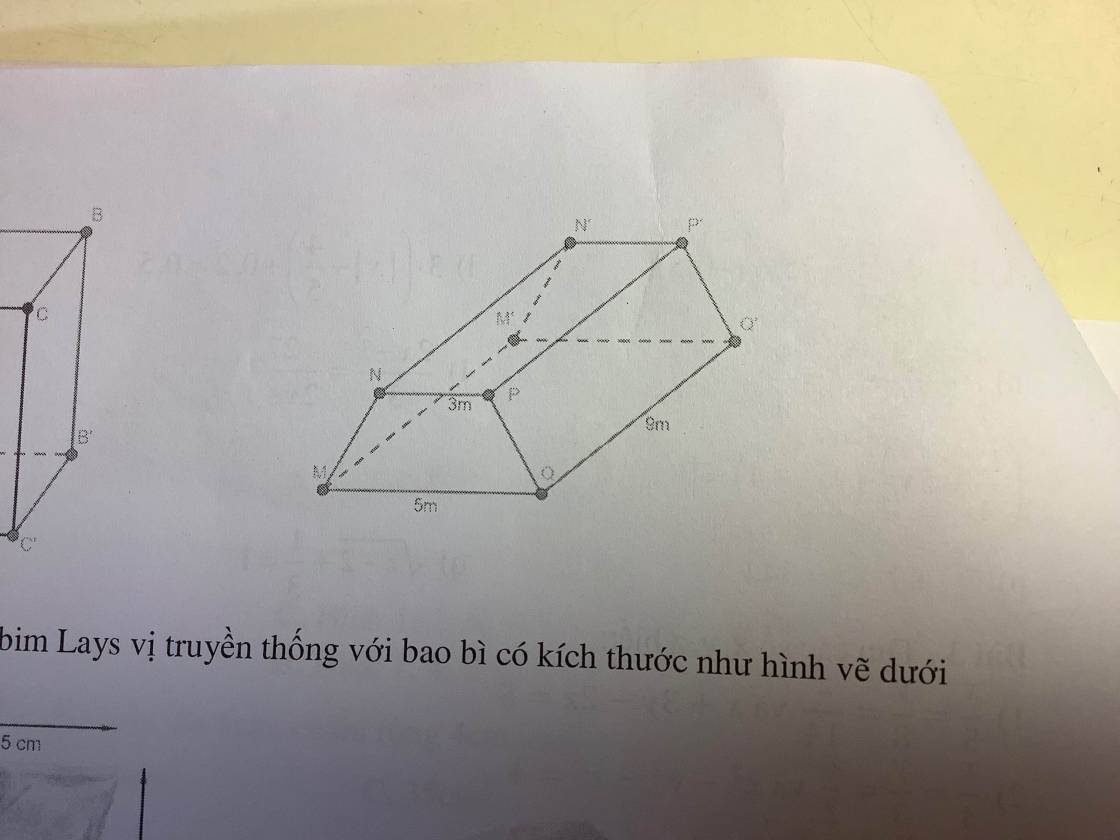
Diện tích xung quanh lăng trụ là :

\(\left(10+2+2.5\right).5=110\left(m^2\right)\)

Diện tích toàn phần lăng trụ là :

\(110+2.\left(10+2\right).3.\dfrac{1}{2}=146\left(m^2\right)\)

Đáp số...

a)

Chu vi đáy hình lăng trụ đứng đó là: 

4+5+6=15 (cm)

Diện tích xung quanh hình lăng trụ đứng đó là:

S_xq = 15.10 = 150 (cm² )

b)

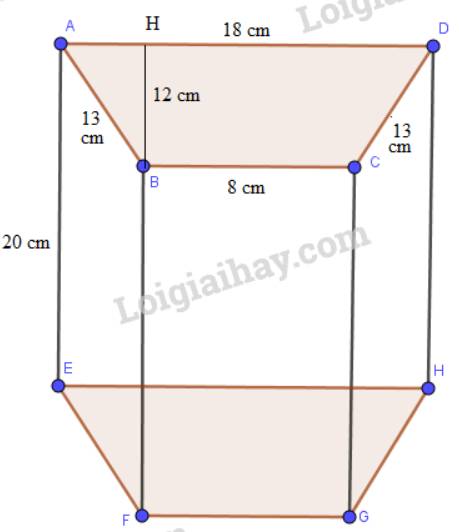
Chu vi đáy là: 8+18+13+13 = 52 (cm)

Diện tích đáy là: S_đáy = (8+18).12:2 = 156 (cm²)

Diện tích toàn phần của lăng trụ đó là:

S_tp = S_xq + 2. S_đáy = 52. 20 +2. 156 = 1352 (cm²)

Gọi chiều cao h và cạnh đáy của hình lăng trụ đứng là a, ta có: Diện tích xung quanh của hình lăng trụ đứng là 120cm2 => Chu vi đáy của hình lăng trụ đứng là P = 120 : h Vì đáy của hình lăng trụ là tam giác đều nên có thể tính diện tích đáy bằng công thức: S = (a2 * √3) / 4 Vậy diện tích xung quanh của hình lăng trụ đều bằng: 120 = P * h = (a * √3) / 4 * h => a = 8√5 và h = 15√3 Vậy chiều cao của hình lăng trụ đứng đó là 15√3, độ dài cạnh đáy của hình lăng trụ là 8√5.

S xq=120cm²

=>h*3a=120cm²

=>h*a=40cm²

=>\(\left(h,a\right)\in\left\{\left(1;40\right);\left(2;20\right);\left(4;10\right);\left(5;8\right);\left(8;5\right);\left(10;4\right);\left(20;2\right);\left(40;1\right)\right\}\)