Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2/5 x 1/X + 1/X x 2 = 0,1
1/X x ( 2/5 + 2 ) = 0,1
1/X x 12 / 5 = 0,1
1/X = 0,1 :12/5 = 1/10 : 12/5
1/X = 1/24
Vậy X = 24

may người do tra loi
the lop 5 sao hiu
ta co: s tam giac
CDA=1/2 s tam giac CAB
(chung chieu cao ha tu c,
day AD=1/2AB)
=>s tam giac CAD
=90/2=45m vuong
Mat khac ta co:s tam giac
DAE=2/3 s tam giac DAC
(chung chieu cao ha tu d, day AE=2/3AC)
=>s tam giac AED
=2/3*45=30m vuong

Kẻ MK vuông góc AC
\(S_{AME}=\dfrac{1}{2}\cdot MK\cdot AE\)
\(S_{MEC}=\dfrac{1}{2}\cdot MK\cdot EC\)
mà AE=1/4*EC
nên \(S_{AME}=\dfrac{1}{4}\cdot S_{MEC}\)
=>\(S_{MEC}=80\left(cm^2\right)\)

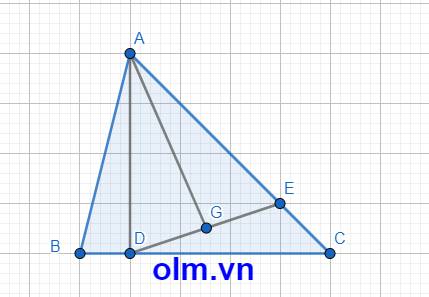
SADE = 2\(\times\)SAGE ( vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy DE và DE = 2\(\times\) GE )
⇒ SADE = 36 \(\times\) 2 = 72 (cm2)
SADE = \(\dfrac{3}{4}\)\(\times\)SADC (vì hai tam giác có chung chiều cao hạ từ Đỉnh D xuống đáy AC và AE = \(\dfrac{3}{4}\)AC)
⇒ SACD = 72 : \(\dfrac{3}{4}\) = 96 (cm2)
DC = BC - BD = BC - \(\dfrac{1}{5}\)BC = \(\dfrac{4}{5}\)BC
SADC = \(\dfrac{4}{5}\)SABC (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và DC = \(\dfrac{4}{5}\)BC)
⇒ SABC = 96 : \(\dfrac{4}{5}\) = 120 (cm2)
Tỉ số phần trăm diện tích tam giác ADE và diện tích tam giác ABC là:
72 : 120 = 0,6
0,6 = 60%
Đáp số: 60%

Bài này hơi khó nên không chắc nhé bạn ==*
Tứ giác ADHE có 3 góc vuông nên nó là hình chữ nhật
Suy ra: AH = DE ( tính chất hình chữ nhật )
Tam giác ABC vuông tại A và có AH là đường cao
Theo hệ thức giữa đường cao và hình chiếu ta có:
AH2 = HB . HC = 4 . 9 = 36 => AH = 6 ( cm )
Vậy DE = 6 ( cm )
b. *Gọi G là giao điểm của AH và DE
Ta có: GA = GD = GH = GE (tính chất hình chữ nhật)
Suy ra tam giác GHD cân tại G
Ta có : \(\widehat{GDH}=\widehat{GHD}\left(1\right)\)
\(\widehat{GDH}+\widehat{MDH}=90^o\left(2\right)\)
\(\widehat{GHD}+\widehat{MHD}=90^o\left(3\right)\)
Từ (1) (2) và (3) , suy ra : \(\widehat{MDH}=\widehat{MHD}\left(4\right)\)
\(\Rightarrow\Delta MDH\)cân tại M \(\Rightarrow MD=MH\left(5\right)\)
Ta lại có : \(\widehat{MDH}+\widehat{MDB}=90^o\left(6\right)\)
\(\widehat{MBD}+\widehat{MHD}=90^o(\Delta BHD\)vuông tại D ) ( 7 )
Từ (4) (6) và (7) , suy ra : \(\widehat{MDB}=\widehat{MBD}\)
\(\Rightarrow\Delta MDH\)cân tại M \(\Rightarrow MB=MD\left(8\right)\)
Từ (5) và (8) , suy ra : \(MB=MH\)hay M là trung điểm của BH
*\(\Delta GHE\)cân tại G
Ta có : \(\widehat{GHE}=\widehat{GEH}\left(9\right)\)
\(\widehat{GHE}+\widehat{NHE}=90^o\left(10\right)\)
\(\widehat{GEH}+\widehat{NEH}=90^o\left(11\right)\)
Từ (9) (10) và (11) , suy ra : \(\widehat{NHE}=\widehat{NEH}\left(12\right)\)
\(\Rightarrow\Delta NEH\)cân tại N => NE = NH ( 13 )
Lại có : \(\widehat{NEC}+\widehat{NEH}=90^o\left(14\right)\)
\(\widehat{NHE}+\widehat{NCE}=90^o(\Delta CEH\)vuông tại E ) ( 15 )
Từ (12) (14) và (15) , suy ra : \(\widehat{NDC}=\widehat{NCE}\)
Suy ra tam giác NCE cân tại N ⇒ NC = NE (16)
Từ (13) và (16) suy ra: NC = NH hay N là trung điểm của CH.
c. Tam giác BDH vuông tại D có DM là đường trung tuyến nên :
\(DM=\frac{1}{2}BH=\frac{1}{2}.4=2\left(cm\right)\)
\(\Delta CEH\)vuông tại E có EN là đường trung tuyến nên :
\(EN=\frac{1}{2}CH=\frac{1}{2}.9=4,5\left(cm\right)\)
Mà \(MD\perp DE\)và \(NE\perp DE\)nên MD // NE
Suy ra tứ giác DENM là hình thang
Vậy : \(S_{DENM}=\frac{DM+NE}{2}.DE=\frac{2+4,5}{2}.6=19,5\left(cm^2\right)\)