Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt AI = x (cm) , (x>0) , IC = y (cm) , (y>0)
Ta có : \(2y^2=18,2015\Rightarrow y=\sqrt{\frac{18,2015^2}{2}}\)
Mặt khác : \(x^2+DI^2=AD^2=14,2014^2\) ; \(y^2+DI^2=CD^2=18,2015^2\)
\(\Rightarrow y^2-x^2=18,2015^2-14,2014^2\Rightarrow x=\sqrt{y^2-18,2015^2+14,2014^2}\)
Từ đó dễ dàng giải tiếp bài toán.

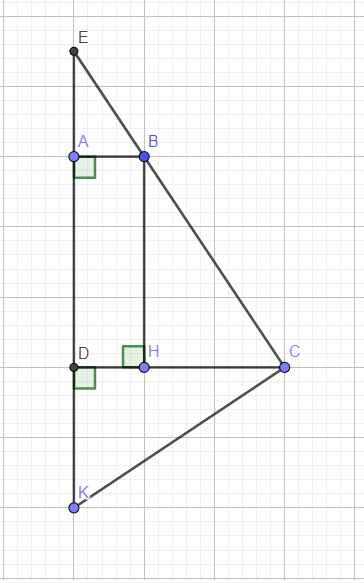
Do \(AD\perp CD\Rightarrow\) hình thang ABCD vuông tại A và D
\(\Rightarrow\) Tứ giác ABHD là hình chữ nhật (tứ giác có 3 góc vuông)
\(\Rightarrow AD=BH\) \(\Rightarrow BH=CD\)
Xét hai tam giác vuông BCH và CKD có:
\(\left\{{}\begin{matrix}BH=CD\\DK=CH\end{matrix}\right.\) \(\Rightarrow\Delta BCH=\Delta CKD\left(c.g.c\right)\) (1)
\(\Rightarrow\widehat{DCK}=\widehat{HBC}\)
\(\Rightarrow\widehat{BCK}=\widehat{BCH}+\widehat{DCK}=\widehat{BCH}+\widehat{HBC}=90^0\)
\(\Rightarrow BC\perp CK\)
b. Cũng từ (1) ta suy ra \(CB=CK\)
Áp dụng hệ thức lượng trong tam giác vuông ECK với đường cao CD:
\(\dfrac{1}{CD^2}=\dfrac{1}{CE^2}+\dfrac{1}{CK^2}=\dfrac{1}{CE^2}+\dfrac{1}{CB^2}\) (đpcm)

Gửi bạn lời giải. Có gì sai sót thì bạn góp ý nhé!
Kẻ \(\)$\(CH \perp AB\)$ tại H, $\(DK \perp AB\)$ tại K.
Áp dụng định lí Pytago vào tam giác ABC vuông tại C, ta có:
$\(AC^2=AB^2-BC^2=26^2-10^2=576\)$
Áp dụng hệ thức lượng vào tam giác ABC vuông tại C với đường cao CH, ta có:
$\(\dfrac{1}{CH^2}=\dfrac{1}{DK^2}=\dfrac{1}{AC^2}+\dfrac{1}{BC^2}=\dfrac{1}{100}+\dfrac{1}{576}=\dfrac{169}{14400}\)$ (do ABCD là hình thang cân)
⇒ $\(CH^2=DK^2=\dfrac{14400}{169}\)$
⇒ $\(CH=DK=\dfrac{120}{13}\)$
Áp dụng định lí Pytago vào tam giác CHB vuông tại H và tam giác AKD vuông tại K có:
$\(BH^2=AK^2=10^2-\dfrac{14400}{169}=\dfrac{2500}{169}\)$ ⇒ $\(BH=AK=\dfrac{50}{13}cm\)$ Ta có: $\(AB=AK+HK+BH=AK+CD+HK\)$ ⇒ $\(CD=AB-AK-HK=26-\dfrac{100}{13}=\dfrac{238}{13}\)$
Ta có: $\({S}_{ABCD}=\dfrac{(AB+CD).AH}{2}=\dfrac{(26+\dfrac{238}{13}).\dfrac{120}{13}}{2}=\dfrac{34560}{169} cm^2\)$