Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\widehat{ABC}=120^0\Rightarrow\widehat{DAB}=180^0-120^0=60^0\)
\(\Rightarrow\Delta ABD\) đều
Gọi E là trung điểm AD \(\Rightarrow\overrightarrow{BE}=\dfrac{1}{2}\overrightarrow{BD}+\dfrac{1}{2}\overrightarrow{BA}\)
\(\Rightarrow\overrightarrow{BG}=\dfrac{2}{3}\overrightarrow{BE}=\dfrac{1}{3}\overrightarrow{BD}+\dfrac{1}{3}\overrightarrow{BA}\)
\(\Rightarrow\overrightarrow{BG}+\overrightarrow{AD}=\dfrac{1}{3}\overrightarrow{BD}+\dfrac{1}{3}\overrightarrow{BA}+\overrightarrow{AD}=\dfrac{1}{3}\left(\overrightarrow{BA}+\overrightarrow{AD}\right)+\dfrac{1}{3}\overrightarrow{BA}+\overrightarrow{AD}\)
\(=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{4}{3}\overrightarrow{AD}=-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{4}{3}\overrightarrow{AD}\)
Đặt \(\overrightarrow{u}=\overrightarrow{BG}+\overrightarrow{AD}\Rightarrow\left|\overrightarrow{u}\right|^2=\left(-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{4}{3}\overrightarrow{AD}\right)=\dfrac{4}{9}AB^2+\dfrac{16}{9}AD^2-\dfrac{16}{9}\overrightarrow{AB}.\overrightarrow{AD}\)
\(=\dfrac{4}{9}.4a^2+\dfrac{16}{9}4a^2-\dfrac{16}{9}.2a.2a.cos60^0=\dfrac{16}{3}a^2\)
\(\Rightarrow\left|\overrightarrow{u}\right|=\dfrac{4a\sqrt{3}}{3}\)

Lời giải:
a. $K$ là giao điểm $AC$ và $BD$ thì $K$ là trung điểm mỗi đường và $AC\perp BD$ tại $K$
Vì $ABCD$ là hình thoi nên $\widehat{DAK}=\frac{1}{2}\widehat{A}=30^0$
$\frac{AK}{AD}=\cos \widehat{DAK}=\cos 30^0=\frac{\sqrt{3}}{2}$
$\Rightarrow AK=\frac{\sqrt{3}}{2}AD=\frac{\sqrt{3}}{2}a$
$\Rightarrow |\overrightarrow{AC}|=AC=2AK=\sqrt{3}a$
b.
$BK=\sqrt{AB^2-AK^2}=\sqrt{a^2-(\frac{\sqrt{3}}{2}a)^2}=\frac{a}{2}$
$S_{ABC}=\frac{BK.AC}{2}=\frac{AH.BC}{2}$
$\Leftrightarrow \frac{a}{2}.\sqrt{3}a=AH.a$
$\Leftrightarrow AH=\frac{\sqrt{3}}{2}a$ hay $|\overrightarrow{AH}|=\frac{\sqrt{3}}{2}a$
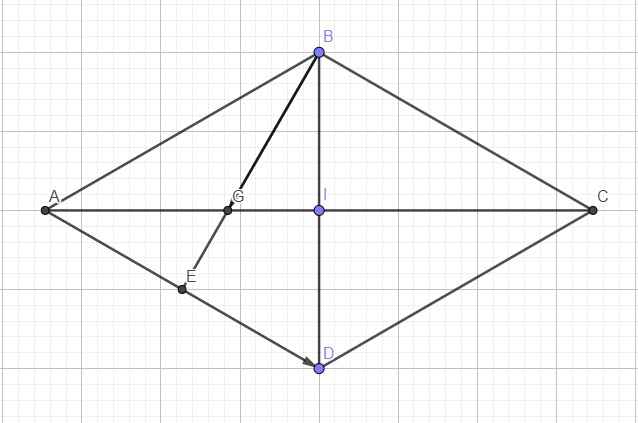
\(\widehat{BAC}=60^0\Rightarrow\) các tam giác ABC và ACD là các tam giác đều
\(\Rightarrow AC=AB=7\)
\(\overrightarrow{AB}.\overrightarrow{AC}=AB.AC.cos\widehat{BAC}=7.7.cos60^0=\dfrac{49}{2}\)
\(\overrightarrow{OA}=-\dfrac{1}{2}\overrightarrow{AC}\Rightarrow\overrightarrow{AB}.\overrightarrow{OA}=-\dfrac{1}{2}\overrightarrow{AB}.\overrightarrow{AC}=-\dfrac{49}{4}\)
\(\overrightarrow{AC}.\overrightarrow{BD}=\overrightarrow{0}\) (do theo tính chất hình thoi ta có \(AC\perp BD\))
\(\overrightarrow{AB}.\overrightarrow{OB}=\overrightarrow{AB}\left(\overrightarrow{OA}+\overrightarrow{AB}\right)=\overrightarrow{AB}.\overrightarrow{OA}+\overrightarrow{AB}^2=-\dfrac{49}{4}+7^2=\dfrac{147}{4}\)