ảnh ở đâu đấy,làm sao vậy chỉ đi

cả bài này đều sử dụng đường trung bình

a) Hình thang ABCD có:

E là trung điểm của AD (1)

F là trung điểm của BC

=> EF là đường trung bình của hình thang ABCD

nên EF// CD

=> EK // CD (2)

Từ (1)(2) => KA = KC

b)  * Xét tam giác ACD có:

EA =ED (gt)

KA = KC (cmt)

=> EK là đường trung bình của tam giác ACD

=>EK = 1/2 CD

=>CD = 6 x 2

 CD= 12 cm

* Tương tự chứng minh KF là đường trung bình của tam giác ABC

=> KF =1/2 AB

=>AB = 2 x 2

AB = 4 cm

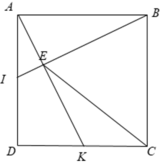
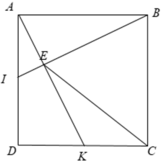
a, Vì \(\left\{{}\begin{matrix}AD=AB\\AI=DK\left(\dfrac{1}{2}AD=\dfrac{1}{2}DC\right)\\\widehat{BAD}=\widehat{ADK}=90^0\end{matrix}\right.\) nên \(\Delta AIB=\Delta DKA\left(c.g.c\right)\)

\(\Rightarrow\widehat{ABI}=\widehat{DAI}\\ \Rightarrow\widehat{DAI}+\widehat{AIB}=\widehat{ABI}+\widehat{AIB}=90^0\\ \Rightarrow BI\perp AK\)

Lời giải:
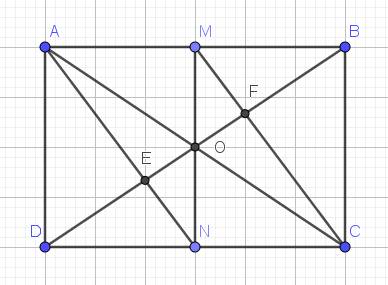
a. Vì $ABCD$ là hình chữ nhật nên $\widehat{A}=\widehat{D}=90^0$

$MN\perp CD$ nên $\widehat{MND}=90^0$
Tứ giác $AMND$ có 3 góc vuông $\widehat{A}=\widehat{D}=\widehat{N}$ nên là hcn.

b. 

Hoàn toàn tương tự phần a ta thấy $\widheat{B}=\widehat{C}=\widehat{N}$ nên $BMNC$ là hcn

$\Rightarrow BM=NC$
$AMND$ là hcn nên $AM=DN$

Mà $AM=BM$ nên $AM=NC$
Có $AM\parallel NC$ (do $AB\parallel CD$) và $AM=NC$ nên $AMCN$ là hbh

$\Rightarrow AC, MN$ cắt nhau tại trung điểm mỗi đường.

Mà $O$ là trung điểm $MN$ nên $O$ cũng là trung điểm $AC$.

c.

Vì $AMCN$ là hbh (theo phần b) nên $AN\parallel CM$

$\Rightarrow EN\parallel FC$
$\Rightarrow \frac{DE}{EF}=\frac{DN}{NC}=1$ (theo định lý Talet)

$\Rightarrow DE=EF(1)$

Mặt khác:

$AN\parallel CM$

$\Rightarrow MF\parallel AE$

$\Rightarrow \frac{BF}{EF}=\frac{BM}{MA}=1$ (định lý Talet)

$\Rightarrow BF=EF(2)$

Từ $(1); (2)\Rightarrow DE=EF=BF$

Hình vẽ: