Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nối \(SB';SC';SD'\) lần lượt cắt \(A'B';A'C';A'D'\) tại M, N, P
\(\Rightarrow M,N,P\) là trung điểm của A'B', A'C', A'D' theo tính chất đường trung bình
\(\Rightarrow A'MNP\) là hình vuông cạnh \(\frac{a}{2}\)
\(V_{A'MNP.ABCD}=V_{S.ABCD}-V_{S.A'MNP}=\frac{1}{3}\left(SA.AB^2-SA'.AM^2\right)\)
\(=\frac{1}{3}\left(2a.a^2-a.\left(\frac{a}{2}\right)^2\right)=\frac{7a^3}{12}\)

Chọn B
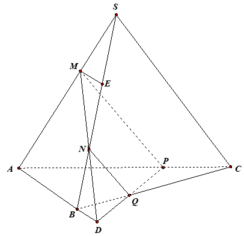
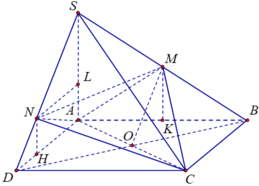
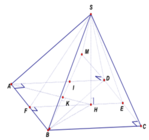
Trong mặt phẳng (SAC) dựng MP song song với SC cắt AC tại P. Trong mặt phẳng (SBC) dựng NQ song song với SC cắt BC tại Q. Gọi D là giao điểm của MN và PQ. Dựng ME song song với AB cắt SB tại E (như hình vẽ).
Ta thấy: ![]()
Suy ra N là trung điểm của BE và DM, đồng thời
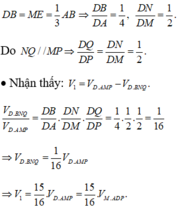
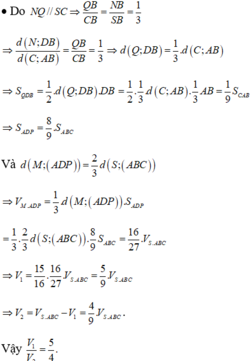

Chọn D
Thể tích khối chóp S. ABCD là:
![]()
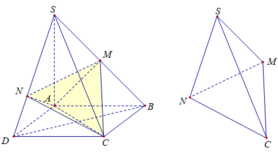
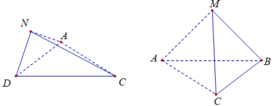
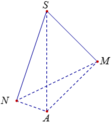
Thể tích tứ diện SMNC là:
![]() .
.
Thể tích tứ diện NACD là:
![]() .
.
Thể tích tứ diện MABC là:
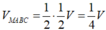 .
.
Thể tích tứ diện SAMN là:
![]() .
.
Mặt khác ta có:
![]()
Suy ra:
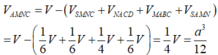

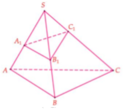
Phương pháp:
Sử dụng công thức tỉ số thể tích cho khối chóp tam giác
(Công thức Simson): Cho khối chóp S.ABC, các điểm A 1 , B 1 , C 1
lần lượt thuộc SA, SB, SC. Khi đó,
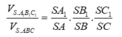
Cách giải:
Dựng ![]()
![]()
![]()
=> MNPQ là thiết diện cần dựng.
V i là thể tích khối đa giác SNM.APQ
![]()
Khi đó, khối đa giác SNM.APQ được chia làm 2 phần:
khối chóp tam giác S.RMN và khối lăng trụ RMN.AQP.
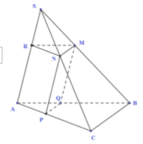
Giả sử S M S B = x
Ta có: 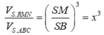
![]()
![]()
![]()
![]()
Mà V 1 V = 20 27
![]()
![]()
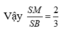
Chọn: A
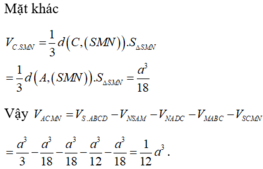
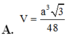
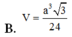





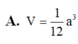
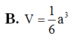
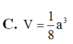
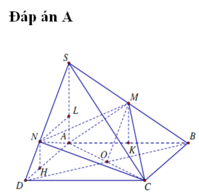

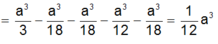
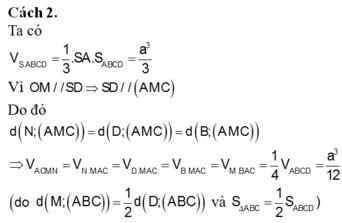
Gọi giao của SB với \(A'B'\) là M, giao của \(SD\) với \(A'D'\) là N
\(\Rightarrow M,N\) lần lượt là trung điểm A'B' và A'D'
\(\Rightarrow\Delta MA'N\) vuông cân tại A' với \(A'M=A'N=\frac{a}{2}\)
\(V_{A'MN.ABD}=V_{S.ABD}-V_{SA'MN}=\frac{1}{6}\left(SA.AB^2-SA'.A'M^2\right)\)
\(=\frac{1}{6}\left(2a.a^2-a.\left(\frac{a}{2}\right)^2\right)=\frac{7a^3}{24}\)