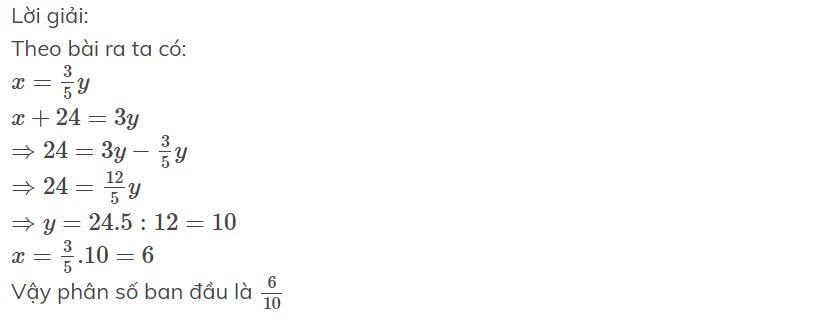Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Theo bài ra ta có:
$x=\frac{3}{5}y$
$x+24=3y$
$\Rightarrow 24=3y-\frac{3}{5}y$
$\Rightarrow 24 = \frac{12}{5}y$
$\Rightarrow y=24.5:12=10$
$x=\frac{3}{5}.10=6$
Vậy phân số ban đầu là $\frac{6}{10}$

Phân số hữu hạn là : \(\frac{5}{8}=0.625,-\frac{3}{20}=-0.15\)\(\frac{14}{35}=\frac{2}{5}=0.4\) vì mẫu tối giản của chúng là tích của các lũy thừa 2 và 5.
Phân số còn lại là vô hạn tuần hoàn vì mẫu của chúng không phân tích được thành tích của các lúy thừa 2 và 5.
Số \(\frac{4}{11}=0.\left(36\right),\frac{15}{22}=0.68\left(18\right),-\frac{7}{12}=-0.58\left(3\right)\)

Ta có : \(\frac{a}{b}\)=\(\frac{-7}{15}\)=> \(\frac{-a}{7}\)=\(\frac{b}{15}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{-a}{7}\)=\(\frac{b}{15}\)=\(\frac{-a+b}{7+15}\)=\(\frac{220}{22}\)=10
=> \(\frac{-a}{7}\)=10 => -a = 70 => a=70
Tương tự b =150
Vậy \(\frac{a}{b}\)=\(\frac{-70}{150}\)

Gọi phân số đó là \(\frac{a}{b}\) (a; b khác 0)
ta có: a+ b = 378
và \(\frac{a}{b}\) = \(\frac{2}{7}\) => \(\frac{a}{2}=\frac{b}{7}\). Theo tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{2}=\frac{b}{7}=\frac{a+b}{2+7}=\frac{378}{9}=42\)
=> a = 42.2 = 84
b = 42 . 7 = 294
ĐS:...
Tổng số phần là :
2 + 7 = 9 ( phần )
Tử số của phân số đó là :
378 : 9 x 2 = 84
Mẫu số của phân số đó là :
378 - 84 = 294
Vậy phân số đó là \(\frac{84}{294}\)

a) Đặt \(ƯCLN\left(5a+3,7a+4\right)=d\)
\(\Rightarrow\left\{{}\begin{matrix}5a+3⋮d\\7a+4⋮d\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}35a+21⋮d\\35a+20⋮d\end{matrix}\right.\)
\(\Rightarrow\left(35a+21\right)-\left(35a+20\right)⋮d\)
\(\Rightarrow1⋮d\)
\(\Rightarrow d=1\)
Vậy \(ƯCLN\left(5a+3,7a+4\right)=1\) hay phân số \(\dfrac{5a+3}{7a+4}\) là phân số tối giản. Thế thì phân số này không thể rút gọn cho nguyên nào khác 1.
b) \(A=\dfrac{5a+3}{7a+4}\)
\(A=\dfrac{\dfrac{5}{7}\left(7a+4\right)+\dfrac{1}{7}}{7a+4}\)
\(A=\dfrac{5}{7}+\dfrac{1}{7\left(7a+4\right)}\)
Nếu \(a< 0\) thì \(A< \dfrac{5}{7}\) còn nếu \(a\ge0\) thì \(A>\dfrac{5}{7}\). Do đó ta chỉ cần tìm giá trị lớn nhất của A khi \(a>0\). Để A lớn nhất thì \(7a+4\) nhỏ nhất hay \(a=0\). Vậy để phân số A lớn nhất thì \(a=0\)