Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì ∆ABC cân tại A, AM là đường trung tuyến ứng với cạnh đáy BC nên AM cũng là đường trung trực của BC.
Vì D là giao điểm của các đường trung trực AC và BC nên D thuộc đường trung trực của AB.
Theo tính chất đường trung trực, ta có:
DA = DB.

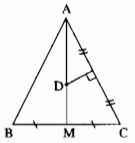
∆ABC cân tại A, AM là đường trung tuyến ứng với cạnh đáy BC nên AM cũng là đường trung trực của BC.
D là giao điểm của các đường trung trực AC và BC nên D thuộc trung trực của AB.
Vậy DA = DB (tính chất đường trung trực).

Vì D nằm trên đường trung trực của AC
nên DA=DC(1)
Xét ΔDBC có
DM là đường cao
DM là đường trung tuyến
Do đó;ΔDBC cân tại D
=>DB=DC(2)
Từ (1) và (2) suy ra DA=DB

∆ABC cân tại A, AM là đường trung tuyến ứng với cạnh đáy BC nên AM cũng là đường trung trực của BC.
D là giao điểm của các đường trung trực AC và BC nên D thuộc trung trực của AB.
Vậy DA = DB (tính chất đường trung trực).
a) Ta có: Đường trung trực của đoạn thẳng AC cắt cắt BC tại F
=> F thuộc đường trung trực của đoạn thẳng AC
=> FA=FC
=> Tam giác ACF cân tại F
Xét tam giác AFC có: FE và AM là hai đường cao cắt nhau tại I
=> I là trực tâm của tam giác AFC
=> CI vuông góc AF
b) Ta có: Tam giác FAC cân tại F
=> \(\widehat{A_1}=\widehat{C_1}\)
Tam giác ABC cân tại A
=> \(\widehat{B_1}=\widehat{C_1}\)
=> \(\widehat{A_1}=\widehat{B_1}\)(1)
Mà \(\widehat{A_1}+\widehat{A_2}=180^o\)( kề bù) (2)
và \(\widehat{B_1}+\widehat{B_2}=180^o\) ( kề bù) (3)
Từ (1), (2), (3) => \(\widehat{A_2}=\widehat{B_2}\)
Xét tam giác ABF và tam giác CAD
có: AB=AC ( tam giác ABC cân)
\(\widehat{A_2}=\widehat{B_2}\)( chứng minh trên)
BF=AD ( giả thiết)
=> Tam giác ABF = tam giác CAD
=> \(\widehat{D}=\widehat{F}\)
=> Tam giác CFD cân tại D
c) CD vuông CF
=> Tam giác CFD vuông cân
=> \(\widehat{AFC}=\widehat{DFC}=45^o\)
Xét tam giác AFC cân tại F
=> \(\widehat{C_1}+\widehat{A_1}+\widehat{AFC}=180^o\Rightarrow\widehat{C_1}=\widehat{A_1}=\frac{180^o-45}{2}=67,5^o\)
Xét tam giác ABC cân tại A
=> \(\widehat{C_1}=\widehat{B_1}=67,5^o\)
=> \(\widehat{A}=45^o\)
Điều kiện của tam giác ABC là cân tại A và góc A bằng 45 độ

a, AM là đường trung tuyến của tam giác cân ABC => BM=MC=1/2 BC = 5
AM là đường trung tuyến của tam giác cân ABC nên AM cũng đồng thời là đường cao trong tam giác này
=> góc AMB = 90độ
Áp dụng định lí Pytago vào tam giác vuông ABM tại M có: \(AM^2=AB^2-BM^2=13^2-5^2=12^2\Rightarrow AM=12\\ \)
b, EF là trung trực AC => FE vuông góc AC và R là trung điểm AC
Hay góc FEC=90độ và EC=EA
Xét tam giác FEC và FEA có:
FE _ cạnh chung
góc FEC = góc FEA = 90độ
EC=EA
=> tg FEC = tg FEA (c-g-c) => FC=FA => tg FAC cận tại F
Xét tg FAC có FE, AM là 2 đường cao trong tam giác và chúng cắt nhau tại I => I là trực tâm tg FAC => CI vuong góc À
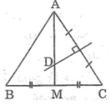
Ta có DA=DC( vì điểm D nằm trên đường trung trực của AC) (1)
Ta có \(AM⊥BC\), vì trong tam giác cân, đường trung tuyến đồng thời là đường phân giác
=> \(\widehat{AMB}=\widehat{AMC}=90\) độ hay \(\widehat{DMB}=\widehat{DMC}=90\) độ
=> Tam giác DMB và tam giác DMC vuông tại M
Xét tam giác DMB và tam giác DMC có
BM=MC( vì AM là đường trung tuyến của tam giác ABC)
Cạnh DM chung
=> Tam giác DMB=tam giác DMC( 2 cạnh góc vuông)
=>DB=DC (2)
Từ (1) và (2) => DA=DB
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)