Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho tam giác ABC cân ở A, đường trung tuyến AM.
a) Chứng minh AM BC
b) Tính AM biết rằng AB cm BC cm 10 , 12

a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông gócBC

a)
Sửa đề: ΔBIM=ΔCKM
Xét ΔBIM vuông tại I và ΔCKM vuông tại K có
BM=CM(M là trung điểm của BC)
\(\widehat{IBM}=\widehat{KCM}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔBIM=ΔCKM(cạnh huyền-góc nhọn)

Tham khảo:

Xét tam giác ABM và tam giác ACM có :
AM chung
BM = CM ( M là trung điểm BC )
AB = AC (tam giác ABC cân tại A theo giả thiết)
\( \Rightarrow \Delta AMB = \Delta AMC (c-c-c)\)
\( \Rightarrow \widehat{BAM}= \widehat{CAM}\) (2 góc tương ứng)
\( \Rightarrow \) AM thuộc tia phân giác của góc A
Mà AM cắt tia phân giác góc B tại I
\( \Rightarrow \) I là giao của các đường phân giác trong tam giác ABC
\( \Rightarrow \) CI là phân giác góc C (định lí 3 đường phân giác cắt nhau tại 1 điểm)

a: Xet ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC
ΔADE cân tại A
mà AM là đường cao
nên AM là phân giác của góc DAE
c: Xet ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc HAB=góc KAC
=>ΔAHB=ΔAKC
d: Xét ΔAED có
AH/AD=AK/AE
nên HK//DE

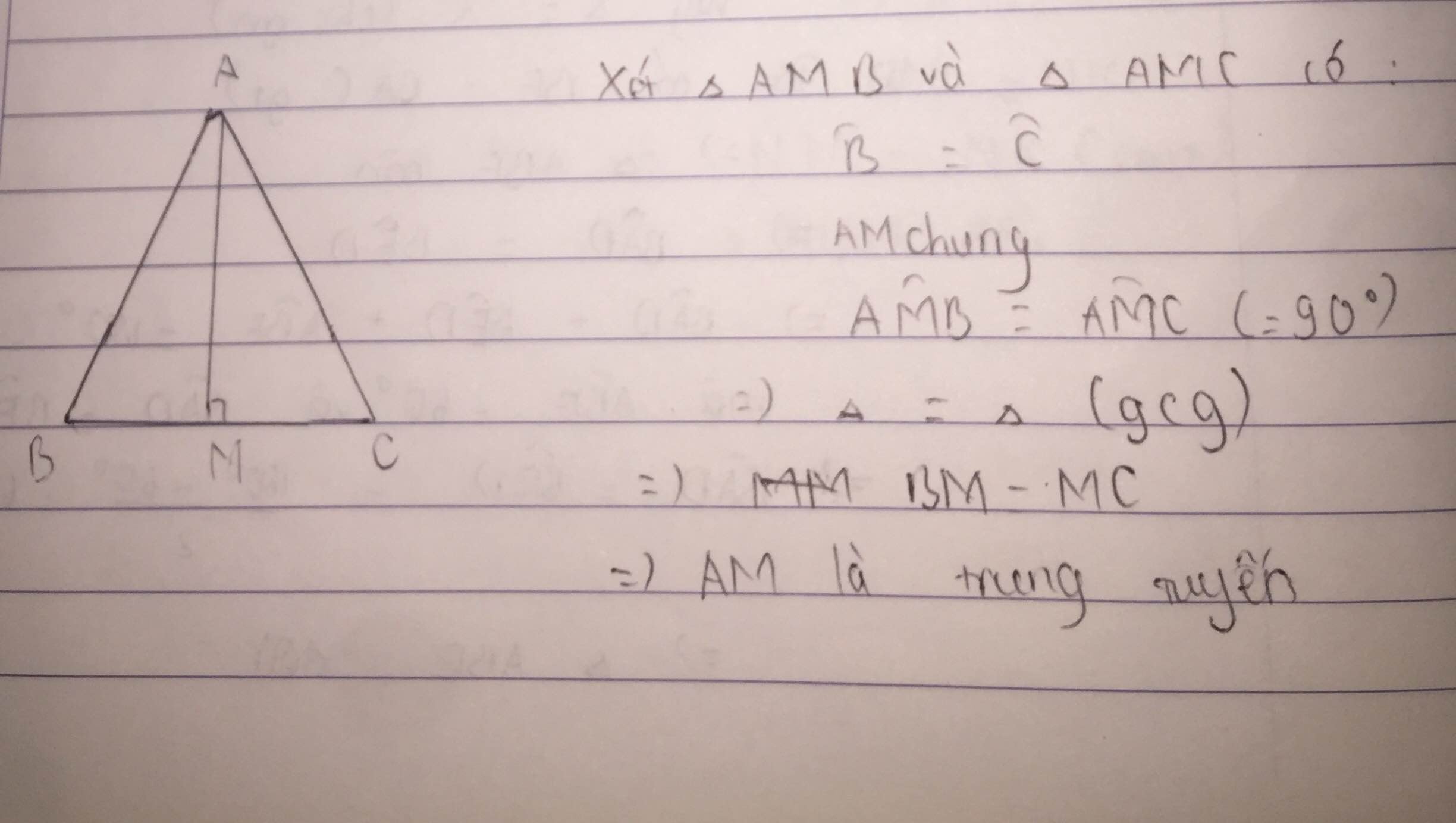
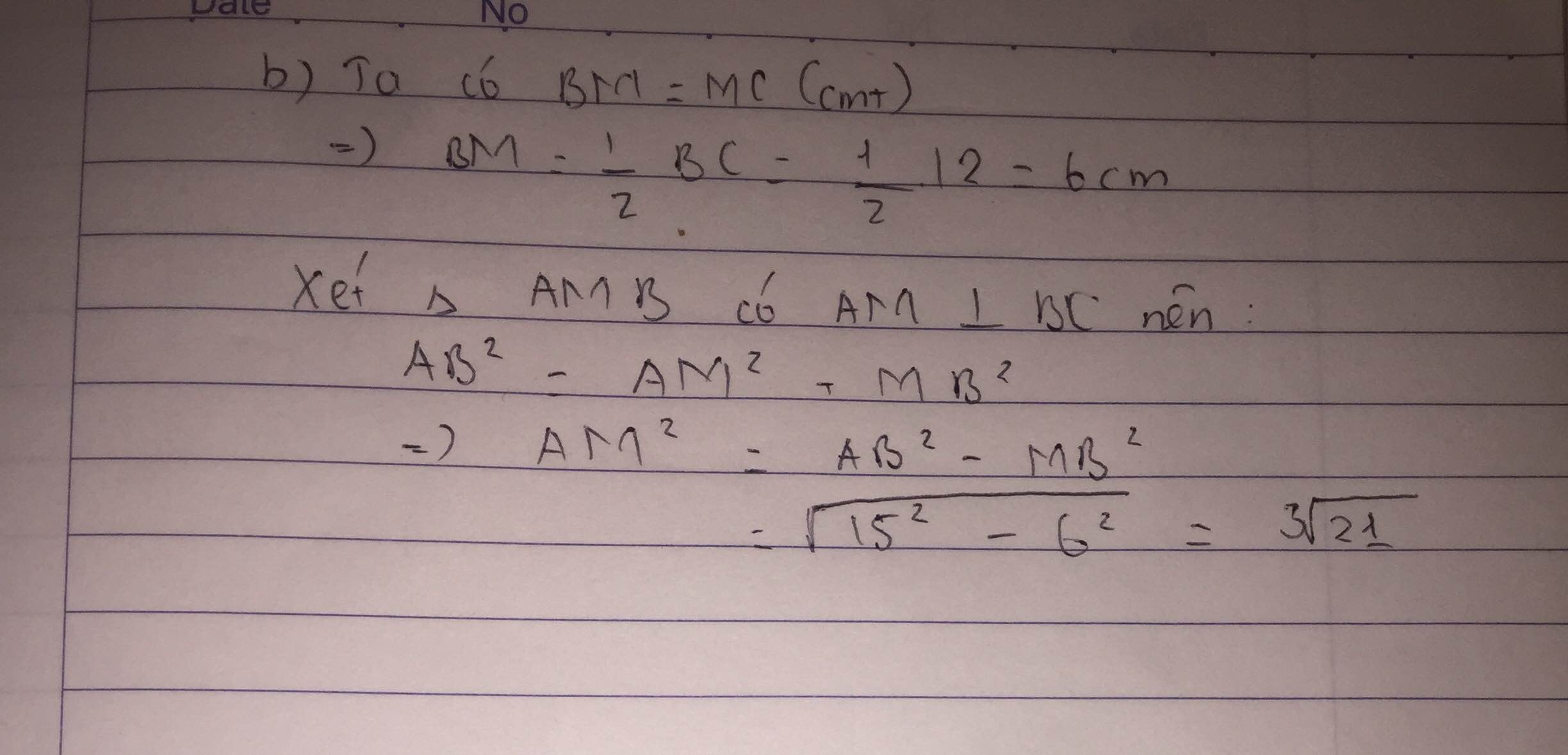


a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác
b: BM=CM=BC/2=6cm
nên AM=8(cm)
a, Ta có AM là trung tuyến của tam giác cân ABC =>AM Đồng thời là đường phân giác và đường trung trực.
b, T a có AM là đường trung trực của tam giác ABC=> góc AMC= 90độ
=> BM=CM=1/2BC=1/2x12=6(cm)
Áp dụng định lý py ta go vào tam giác vuông AMC ta có
AM2+CM2=AC2thay CM=6cm(CMT); AC=10cm(GT)
=>AM2+62=102
=>AM2+36=100
=>AM2 = 100-36=64=82
=>AM =8(cm)