Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông gócBC

a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác
b: BM=CM=BC/2=6cm
nên AM=8(cm)
a, Ta có AM là trung tuyến của tam giác cân ABC =>AM Đồng thời là đường phân giác và đường trung trực.
b, T a có AM là đường trung trực của tam giác ABC=> góc AMC= 90độ
=> BM=CM=1/2BC=1/2x12=6(cm)
Áp dụng định lý py ta go vào tam giác vuông AMC ta có
AM2+CM2=AC2thay CM=6cm(CMT); AC=10cm(GT)
=>AM2+62=102
=>AM2+36=100
=>AM2 = 100-36=64=82
=>AM =8(cm)

a)

Xét 2 tam giác vuông AMC và AMB có:
AM chung
BM=CM (gt)
=>\(\Delta AMC = \Delta AMB\) (hai cạnh góc vuông)
=> AC=AB (2 cạnh tương ứng)
=> Tam giác ABC cân tại A
b)

Kẻ MH vuông góc với AB (H thuộc AB)
MG vuông góc với AC (G thuộc AC)
Xét 2 tam giác vuông AHM và AGM có:
AM chung
\(\widehat {HAM} = \widehat {GAM}\) (do AM là tia phân giác của góc BAC)
=>\(\Delta AHM = \Delta AGM\) (cạnh huyền – góc nhọn)
=> HM=GM (2 cạnh tương ứng)
Xét 2 tam giác vuông BHM và CGM có:
BM=CM (giả thiết)
MH=MG(chứng minh trên)
=>\(\Delta BHM = \Delta CGM\)(cạnh huyền – cạnh góc vuông)
=>\(\widehat {HBM} = \widehat {GCM}\)(2 góc tương ứng)
=>Tam giác ABC cân tại A.

Lời giải:
a.
Do tam giác $ABC$ cân tại $A$ nên $AB=AC$
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$
$AM$ chung
$BM=CM$ (do $M$ là trung điểm $BC$)
$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)
b.
Từ tam giác bằng nhau phần a suy ra $\widehat{BAM}=\widehat{CAM}$. Mà $AM$ nằm giữa $AB, AC$ nên $AM$ là tia phân giác $\widehat{BAC}$
Cũng từ tam giác bằng nhau phần a suy ra:
$\widehat{AMB}=\widehat{AMC}$
Mà $\widehat{AMB}+\widehat{AMC}=\widehat{BMC}=180^0$
$\Rightarrow \widehat{AMB}=180^0:2=90^0$
$\Rightarrow AM\perp BC$
c.
$AM\perp BC, M$ là trung điểm $BC$ nên $AM$ là đường trung trực của $BC$
$\Rightarrow$ mọi điểm $E\in AM$ đều cách đều 2 đầu mút B,C (theo tính chất đường trung trực)
$\Rightarrow EB=EC$
$\Rightarrow \triangle EBC$ cân tại $E$.

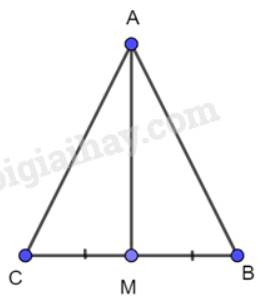
Xét 2 tam giác AMB và AMC có:
AM chung
AB=AC (do tam giác ABC cân tại A)
MB=MC (gt)
\(\Rightarrow\) \(\Delta AMB=\Delta AMC\) (c.c.c)
\(\Rightarrow\) \(\widehat {BAM} = \widehat {CAM}\)(2 góc tương ứng).
Mà tia AM nằm trong góc BAC
\(\Rightarrow\) AM là phân giác của góc BAC
Mặt khác: Do \(\Delta AMB=\Delta AMC\) nên \(\widehat {AMB} = \widehat {AMC}\)(2 góc tương ứng) mà \(\widehat {AMB} + \widehat {AMC} = {180^o}\)( 2 góc kề bù)
Nên: \(\widehat {AMB} = \widehat {AMC} = {90^o}\).
Vậy AM vuông góc với BC.

a: ΔABM=ΔACM
=>BM=CM
=> M là trung điểm của BC
b: ΔAMC=ΔAMB
=>góc MAC=góc MAB và AC=AB
=>AM là phân giác của góc BAC
AB=AC
MB=MC
=>AM là trung trực của BC
=>AM vuông góc BC

Chú ý:Góc ngoài tam giác bằng tổng số đo 2 góc trog tam giác không kể với nó
Vậy góc(A1)+góc(A2)=góc(B)+góc(C) .(1)
Do Am là tia phân giác ngoài tại đỉnh A của tam giác ABC nên góc A1=góc (A2).(2)
Lại có tam giác ABC cân tại A do(AB=AC) nên góc (B)=góc(C).(3)
Từ(1);(2) và (3) =>góc(A1)+góc (A1)=góc (C)+góc(C)
Suy ra góc( A1)=góc(C) mà 2 góc này nằm ở vị ttrí so le nhau
Do đó Am//BC . (dpcm)
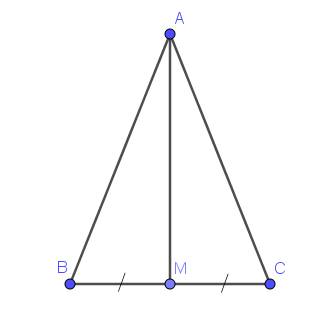


a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông gócBC
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông gócBC