Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b/ Bn tu ve hinh, duong ke phu AH la p/g goc A
Xet \(\Delta ABH\)va \(\Delta ACH\),co:
\(AB=AC\)(GT)
\(\widehat{BAH}=\widehat{CAH}\)(AH la tia p/g goc A)
\(AHchung\)
\(\Rightarrow\Delta ABH=\Delta ACH\left(c.g.c\right)\)
\(\Rightarrow\widehat{B}=\widehat{C}\left(dpcm\right)\)

bn ko giúp thì thoy thì đừng có nói nha,thì đúng là mk học giốt ko bít giải mới đăng lên đấy chứ có ai mà giỏi hết đâu,đây là trang web học tập giúp đỡ nhau nhưng bn ko giúp thì cũng đừng có nói nha

a: Xét ΔABN và ΔACM có
AB=AC
góc BAN chung
AN=AM
Do đó; ΔABN=ΔACM
b: ta có: ΔABC cân tại A
nên \(\widehat{ABC}=\widehat{ACB}\)
c: Xét ΔMBC và ΔNCB có
MB=NC
BC chung
MC=NB
Do đó: ΔMBC=ΔNCB
Suy ra: \(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
Ta có: AB=AC
IB=IC
Do đó: AI là đường trung trực của BC

Mk chụp thiếu 1 dòng rồi bn ạ... Sau cái chỗ tam giác AMI = tam giác ANI bn thêm vào là góc AIN = góc AIM nhé

a. Hình vẽ (0.5 điểm)
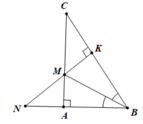
Xét ΔABM và ΔKBM có:
∠(ABM) = ∠(KBM)
BM là cạnh chung
⇒ ΔABM = ΔKBM(cạnh huyên – góc nhọn) (1 điểm)
⇒ AM = MK và BA = BK (hai cạnh tương ứng) ⇒ M, B nằm trên đường trung trực của AK (0.5 điểm)
Suy ra BM là đường trung trực của AK

Xét Δ BDA vuông tại a, ΔBDN vuông tại N có
BD: cạnh huyền chung
\(\widehat{ABD}\)=\(\widehat{NBD}\) (d là tia phân giác của góc B)
⇒ΔBDA=ΔBDN (c.huyền-g.nhọn)
⇒AB=AN (2 góc tương ứng)
2 đt ND va BC sao giao tai M đc bạn. Bạn coi lại đề nha

Xét tam giác ABH có : MI song song với BH, M là trung điểm của AB => I là trung điểm của AH
Xét tam giác AMH có MI vuông góc với AH và MI là đường trung tuyến ứng với AH của tam giác. Do đó tam giác AMH cân tại M
Suy ra MI hay MN là phân giác của AMH

a, Tam giác \(ABC\) cân tại \(A\)
\(\Rightarrow AB=AC;\widehat{B}=\widehat{C}\)
Xét \(\Delta ABM;\Delta ACM\) có
\(AB=AC\left(cmt\right)\\ \widehat{B}=\widehat{C}\left(cmt\right)\\ MB=MC\)
\(\Rightarrow\Delta ABM=\Delta ACM\left(c-g-c\right)\)
b, \(\Delta ABM=\Delta ACM\left(cmt\right)\)
\(\Rightarrow\widehat{HAM}=\widehat{KAM}\)
Xét \(\Delta AHM;\Delta AKM\) có
\(\widehat{HAM}=\widehat{KAM}\left(cmt\right)\\ \widehat{AHM}=\widehat{AKM}=90^o\)
\(AM\) chung
\(\Rightarrow\Delta AHM=\Delta AKM\left(ch-gn\right)\)
\(\Rightarrow HM=KM\)



