Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

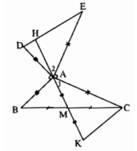
Xét ΔAMB và ΔKMC có:
AM = MK (giả thiết)
BM = MC (vì M là trung điểm của BC)
∠AMB = ∠KMC (hai góc đối đỉnh)
⇒ ΔAMB = ΔKMC (c.g.c)
⇒ ∠ABM = ∠KCM (hai góc t.ư) và AB = CK
⇒ CK // AB (có cặp góc so le trong bằng nhau
+ Ta có: ∠BAM + ∠CAM = 110º ⇒ ∠AKC + ∠CAM = 110º (1)
Xét tam giác ACK có:
∠AKC + ∠CAM + ∠ACK = 180º ( tổng ba góc trong một tam giác). (2)
Từ (1) và (2) suy ra: ∠ACK = 180º - 110º = 70º

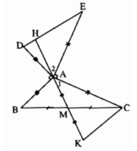
Gọi H là giao điểm của MA và DE.
ΔCAK = ΔAED nên ∠A1 = ∠E. (3)
+) Ta có: ∠A1 + ∠CAE + ∠A2 = 180º
Thay số: ∠A1 + 90º + ∠A2 = 180º ⇒ ∠A1 + ∠A2 = 90º (4)
Từ (3) và( 4) suy ra: ∠A2 + ∠E = 90º
Do đó MA ⊥ DE.

a: Xét tứ giác ABNC có
M là trung điểm của AN
M là trung điểm của BC
Do đó:ABNC là hình bình hành
Suy ra: AB=NC

Xét tam giác ABM và tam giác KCM ta có
AM=MK (gt)
BM=MC (M là trung điểm BC)
góc AMB= góc KMC ( 2 góc đối đỉnh)
=> tam giác ABM = tam giác KCM (c-g-c)
-> góc ABM = góc KCM ( 2 góc tương ứng)
mà 2 góc ở vị trí sole trong
nên AB//CK
=> góc BAC + góc ACK =180 ( 2 góc trong cùng phía)
-> 60+ góc ACK=180
-> góc ACK =180 -60=120
110 độ
Tik cho mk nha..........cảm ơn rất nhiều